Surfc(X,Y,M3); colormap gray

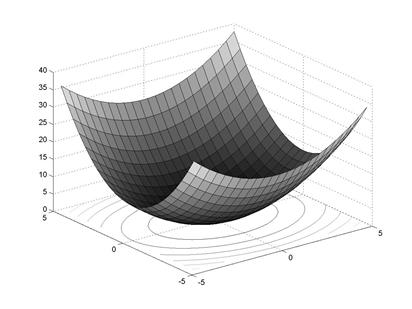
Рис. 4.3. Поверхность и карта линий уровня функции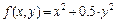

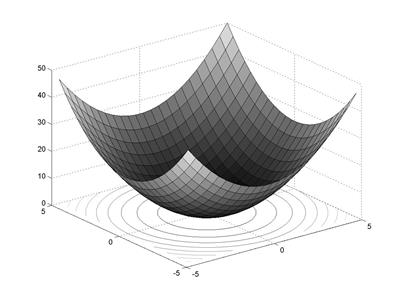
Рис. 4.4. Поверхность и карта линий уровня функции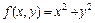

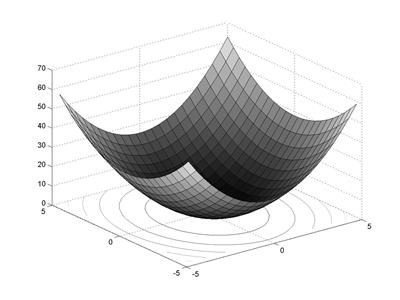
Рис. 4.5. Поверхность и карта линий уровня функции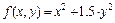

Из рис. 4.3-4.5 видно, что при 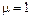функция представляет собой параболоид вращения, при 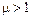параболоид становится эллиптическим, «вытягиваясь» вдоль оси оХ (при 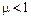- вдоль оси оY).

3. Создание файла Dx_F_L4.m, содержащего описание функции, возвращающей значения частной производной, по переменной x.

% листинг файла Dx_F_L4.m

function z=Dx_F_L4(x,y,mu)

N=length(x);

z=zeros(N);

i=1:N;

j=1:N;

for i=1:N

for j=1:N

z(i,j)=2*x(i);

End;

End;

4. Создание файла Dy_F_L4.m, содержащего описание функции, возвращающей значения частной производной, по переменной y.

% листинг файла Dy_F_L4.m

function z=Dy_F_L4(x,y,mu)

N=length(x);

z=zeros(N);

i=1:N;

j=1:N;

for i=1:N

for j=1:N

z(i,j)=2*mu*x(i);

End;

End;

5. Создание файла L_Grad.m, содержащего описание функции, возвращающей длину градиента функции f(x,y,m)

% листинг файла L_Grad.m

function z=L_Grad(x,y,mu)

N=length(x);

z=zeros(N);

for i=1:N

for j=1:N

z(i,j)=Dx_F_L4(x(i),y(j),mu).^2+Dy_F_L4(x(i),y(j),mu).^2;

z(i,j)=z(i,j).^0.5;

End;

End;

6. Создание файла S_x.m, содержащего описание функции, возвращающей значение проекции на ось oX нормированного единичного вектора, сонаправленного с вектором, направление которого противоположно направлению вектора градиента

% листинг файла S_x.m

function z=S_x(x,y,mu);

N=length(x);

z=zeros(N);

i=1:N;

j=1:N;

for i=1:N

for j=1:N

z(i,j)=-Dx_F_L4(x(i),y(j),mu)./L_Grad(x(i),y(j),mu);

End;

End;

7. Создание файла S_y.m, содержащего описание функции, возвращающей значение проекции на ось oY нормированного единичного вектора, сонаправленного с вектором, направление которого противоположно направлению вектора градиента

% листинг файла S_y.m

function z=S_y(x,y,mu);

N=length(x);

z=zeros(N);

for i=1:N

for j=1:N

z(i,j)=-Dy_F_L4(x(i),y(j),mu)./L_Grad(x(i),y(j),mu);

End;

End;

8. Создание файла Lambda.m, содержащего описание функции, возвращающей значение шага

% листинг файла Lambda.m

function z=Lambda(x,y,nu,alpha,beta,gamma,lambda0);

z=alpha*lambda0/(beta+gamma*nu);

9. Создание файла MG.m, содержащего описание функции, возвращающей значения переменных x,y и соответствующее значение функции f(x,y,m) на каждом шаге итерационного процесса

% листинг файла MG.m

function [X,Y,ff]=MG(x0,y0,mu,nu,alpha,beta,gamma,lambda0)

X(1)=x0;

Y(1)=y0;

ff(1)=F_L4(x0,y0,mu);

for i=2:nu

X(i)=X(i-1)+Lambda(X(i-1),Y(i-1),nu,alpha,beta,gamma,…

lambda0)*s_x(X(i-1),Y(i-1),mu);

Y(i)=Y(i-1)+Lambda(X(i-1),Y(i-1),nu,alpha,beta,gamma,…

ambda0)*s_y(X(i-1),Y(i-1),mu);

ff(i)=F_L4(X(i),Y(i),mu);

end;

10. Нахождение минимума функции f(x,y,m) и визуализация итерационного процесса

Vmax=20; % максимальное число шагов итерационного процесса

x0=2; y0=-1; % начальное приближение

lambda0=0.3; % начальное значение шага к экстремуму

beta=1; alpha=1; gamma=1;% параметры, используемые для

% определения шага

mu=1;nu=20;

[X,Y,ff]=MG(x0,y0,mu,nu,alpha,beta,gamma,lambda0);