Итераций

Пусть требуется решить систему уравнений

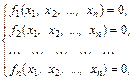(4.1)

где 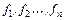- заданные, вообще говоря, нелинейные вещественнозначные функции n вещественных переменных .

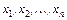Введя обозначения

,

,

,

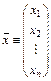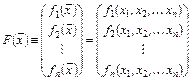систему (4.1) можно заменить одним уравнением

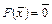(4.2)

относительно векторной функции F векторного аргумента .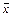

Таким образом, исходную задачу можно рассматривать как задачу о нулях нелинейного отображения 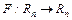. В такой постановке данная задача является прямым обобщением задачи о нахождении решения нелинейного уравнения для случая пространств большей размерности. Это означает, что можно строить методы ее решения, как на основе обсужденных в предыдущей лекции подходов, так и осуществлять формальный перенос выведенных для скалярного случая расчетных формул. Однако не все результаты и не все методы оказывается возможным перенести формально (например, метод половинного деления). В любом случае следует позаботиться о правомерности тех или иных операций над векторными переменными и векторными функциями, а так же о сходимости получаемых таким способом итерационных процессах. Отметим, что переход от n = 1 к n ³ 2 вносит в задачу нахождения нулей нелинейного отображения свою специфику, учет которой привел к появлению новых методов и различных модификаций уже имеющихся методов. В частности, большая вариативность методов решения нелинейных систем связана с разнообразием способов которыми можно решать линейные алгебраические задачи, возникающие при пошаговой линеаризации данной нелинейной вектор-функции .

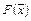Начнем изучение методов решения нелинейных систем с метода простых итераций.

Пусть система (4.1) преобразована к следующей эквивалентной нелинейной системе

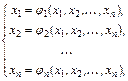(4.3)

или в компактной записи:

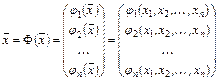. (4.4)

Для этой задачи о неподвижной точке нелинейного отображения 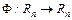запишем формальное рекуррентное равенство

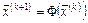, (4.5)

где 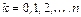, которое определяет метод простых итераций для задачи (4.3).

Если начать процесс построения последовательности 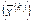с некоторого вектора 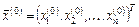и продолжить вычислительный процесс по формуле (4.5), то при определенных условиях данная последовательность со скоростью геометрической прогрессии будет приближаться к вектору 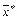- неподвижной точке отображения .

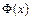Справедлива следующая теорема, которую мы приводим без доказательства.

Теорема 4.1. Пусть функция 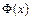и замкнутое множество 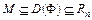таковы, что:

1) ;

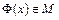
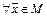2) : .

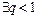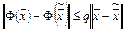
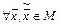Тогда 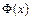имеет в M единственную неподвижную точку 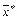; последовательность 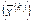, определяемая (4.5), сходится при любом 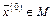к 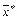и справедливы оценки

.

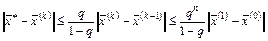
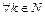Отметим низкую практическую ценность данной теоремы из-за неконструктивности ее условий. В случаях, когда выбрано хорошее начальное приближение 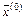решению 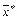, больший практический интерес представляет следующая теорема.

Теорема 4.2. Пусть 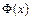дифференцируема в замкнутом шаре , причем 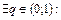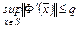. Тогда если центр 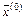и радиус 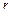шара S таковы, что , то справедливо заключение теоремы 4.1 с .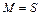

Запишем метод последовательных приближений (4.5) в развернутом виде:

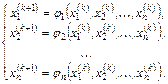(4.6)

Сравнение (4.6) с вычислительной формулой метода простой итерации решения систем линейных уравнений (4.13) обнаруживает их сходство. Учитывая, что в линейном случае, как правило, более эффективным является метод Зейделя, в данном случае также может оказаться более эффективным его многомерный аналог, называемый методом покоординатных итераций:

(4.7)

Заметим, что как и для линейных систем, отдельные уравнения в (4.7) неравноправны, т.е. перемена местами уравнений системы (4.3) может изменить в некоторых пределах число итераций и вообще ситуацию со сходимостью последовательности итераций. Для того чтобы применить метод простых итераций (4.6) или его зейделеву модификацию (4.7) к исходной системе (4.1), необходимо сначала тем или иным способом привести эту систему к виду (4.3). Это можно сделать, например, умножив (4.2) на неособенную n ´ n матрицу A и прибавив к обеим частям уравнения 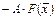вектор неизвестных. Полученная система

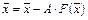(4.8)

эквивалентна исходной и имеет вид, аналогичный уравнению в методе итераций в одномерном случае. Проблема состоит лишь в правильном подборе матричного параметра.