Связь между параметрами последовательных итераций

Выведем формулы пересчёта коэффициентов разложения вектора по базисам двух соседних опорных планов.

Пусть известен опорный план 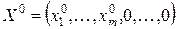с базисом .

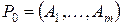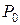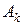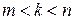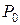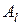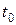Произведём операцию однократного замещения, а именно введем в базис вектор , и выведем из вектор , , т.е. мы предполагаем, что достигается на 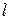-ой позиции:

.

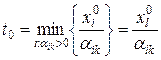Тогда, в результате этой операции однократного замещения, мы получим новый опорный план

координаты которого определяются

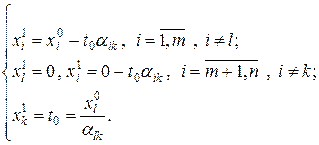
Базис этого опорного плана 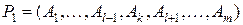, получен из базиса 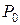заменой столбца на столбец .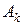

Запишем разложение любого небазисного вектора 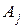по базису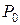

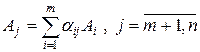. (10.17)

Из системы соотношений (10.17) возьмем

и выразим отсюда (так как 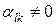по построению опорного плана )

.

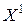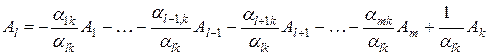Подставим найденное для выражение в (10.17):

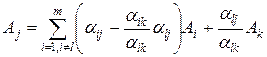. (10.18)

С другой стороны вектор 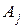, может быть разложен по новому базису

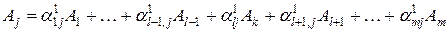(10.19)

Сравнивая (10.18) и (10.19), в силу единственности разложения вектора по базису , получим

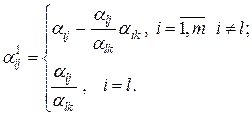(10.20)

Формулы (10.20) позволяют вычислять коэффициенты разложения любого вектора 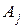по новому базису через коэффициенты разложения его по старому базису .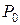

Получим аналогичные рекуррентные формулы для оценок 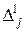небазисных векторов 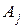относительно нового базиса .

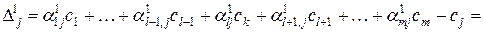
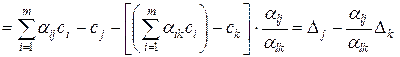
Таким образом

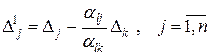(10.21)

Рекуррентные формулы (10.20) и (10.21) являются основой так называемого «первого» алгоритма симплекс - метода решения ЗЛП.

Контрольные вопросы

1. Дайте определения гиперплоскости и верхнего (нижнего) полупространства.

2. Приведите определение опорной гиперплоскости.

3. Опишите графический метод решения ЗЛП.

4. Приведите алгоритм графического метода решения ЗЛП.

5. Перечислите три типовых ситуации, возникающие при решении ЗЛП графическим методом в случае непустого множества допустимых планов.

6. Что лежит в основе метода последовательного улучшения плана?

7. Как осуществляется переход от одного опорного плана к другому опорному плану?

8. Пояснить суть процедуры однократного замещения.

10. Сформулируйте признак оптимальности опорного плана.

11. В чем заключается применение признака оптимальности опорного плана?