Метод Зейделя
При решении системы линейных уравнений вычислительные формулы имеют вид:
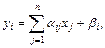 (3.27)
(3.27)
где  .
.
Из (3.27) видно, что в методе простой итерации для получения нового значения вектора решений на i+1-ом шаге используются значения переменных, полученные на предыдущем шаге.
Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении значения переменной 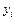 учитываются уже найденные значения
учитываются уже найденные значения 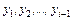 :
:
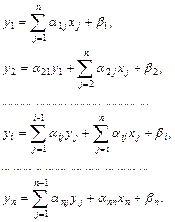 (3.28)
(3.28)
Достаточные условия сходимости итерационного процесса (3.23)-(3.25) также являются достаточным условиями сходимости метода Зейделя.
Существует возможность автоматического преобразования исходной системы к виду, обеспечивающему сходимость итерационного процесса метода Зейделя. Для этого умножим левую и правую части системы (3.2) на транспонированную матрицу системы AT, получим равносильную систему
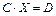 , (3.29)
, (3.29)
где 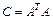 ,
, 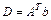 .
.
Система (3.29) называется нормальной системой уравнений. Нормальные системы уравнений обладают рядом свойств, среди которых можно выделить следующие:
1) матрица C коэффициентов при неизвестных нормальной системы является симметрической (т.е. 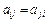 ,
, 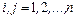 );
);
2) все элементы, стоящие на главной диагонали матрицы C положительны (т.е. 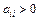 ,
,  ).
).
Последнее свойство дает возможность «автоматически» приводить нормальную систему (3.29) к виду, пригодному для итерационного процесса Зейделя:
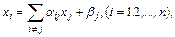 (3.30)
(3.30)
где
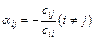 , (3.31)
, (3.31)
и
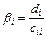 . (3.32)
. (3.32)
Целесообразность приведения системы к нормальному виду и использования метода Зейделя вытекает из следующей теоремы:
Теорема 3.2.Итерационный процесс метода Зейделя для приведенной системы (3.30), эквивалентной нормальной системе (3.29), всегда сходится к единственному решению этой системы при любом выборе начального приближения [2].
Таким образом решение произвольной системы линейных уравнений вида (3.1) методом Зейделя реализуется в соответствие со следующим алгоритмом:
1. Ввод матрицы А коэффициентов исходной системы и вектор-столбца свободных членов.
2. Приведение системы к нормальной умножением обеих частей системы на транспонированную матрицу АT.
3. Приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя (3.30), (3.31).
4. Задание требуемой точности решения.
5. Циклическое выполнение итерационного процесса до достижения требуемой точности.
Для реализации метода Зейделя в пакете MATLAB необходимо:
1. Создать файл Zeidel.m, содержащий описание функции, выполняющей последовательно: а) приведение системы к нормальному виду; б) приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя; в) реализацию итерационного процесса Зейделя.
% листинг файла Zeidel.m
function [z1,z2]=Zeidel(A,b,eps)
N=size(A,1);
% приведение системы к нормальному виду
C=A'*A;
D=A'*b;
% приведение системы к виду пригодному для итерационного процесса
% Зейделя
for i=1:N
D1(i)=D(i)/C(i,i);
End;
D1=D1';% транспонирование матрицы
d1=D1;
for i=1:N
for j=1:N
if i==j
C1(i,j)=0;
Else
C1(i,j)=-C(i,j)/C(i,i);
End;
End;
End;
% решение системы линейных уравнений методом Зейделя
R1=d1;
while Flag==0
for i=1:N
v=C1(i,1:N);% выделение i-oй строки матрицы
a=dot(v',d1);% вычисление скалярного произведения
d1(i)=a+D1(i);
End;
R2=d1;
s=max(abs(R2-R1));
if s<eps
z1=d1;
z2=s;
Return
End;
R1=R2;
End;
2. Задать матрицу коэффициентов при неизвестных исходной системы линейных уравнений и столбец свободных членов
>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]
>> b=[10,20,30,40,50];
3. Вычислить решение системы линейных уравнений, используя функцию Zeidel( )
>> Zeidel1(A,b,10^-6)
ans =
0.0972
1.4325
-1.3533
1.6564
0.8947
4. Проверить полученное решение
>> A*ans
ans =
10.0013
20.0003
29.9995
39.9999
50.0000
3.6. Решение систем линейных уравнений средствами пакета MATLAB
Для решения систем линейных уравнений и связанных с ними матричных операций применяются операторы: сложения (+), вычитания (-), умножения (*), деления справа (/), деления слева (\), возведения в степень (^), транспонирования (¢), действие которых определяется правилами линейной алгебры.
Пусть задана система n линейных алгебраических уравнений с n неизвестными:
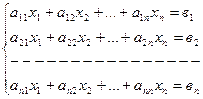 . (3.61)
. (3.61)
Система уравнений (1) в матричной форме представляется следующим образом:
АХ = В, (3.62)
где А – квадратная матрица коэффициентов, размером n ´ n строк и столбцов;
Х – вектор-столбец неизвестных;
В – вектор-столбец правых частей.
Систему уравнений (2) можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невырожденными матрицами, в противном случае метод Гаусса неприменим.
Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n £ 100) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем. Если матрица А сильно разрежена, а ее определитель не близок к нулю, то метод Гаусса не пригоден для решения больших систем уравнений.
В MATLAB имеется обширный арсенал методов решения систем уравнений (2). Для этого применяются следующие операторы
| / | - правое деление; |
| \ | - левое деление; |
| Ù - 1 | - возведение в степень –1; |
| inv(A) | - обращение матрицы А. |
Дата добавления: 2015-08-21; просмотров: 6247;
