Вычисление определителей

Решение системы (3.4) существует только в том случаем, если определитель матрицы A отличен от нуля, поэтому решение любой системы линейных уравнений следует предварять вычислением ее определителя.

Для вычисления определителя используют известное свойство треугольных матриц: определитель треугольной матрицы равен произведению ее диагональных элементов.

Пусть задана квадратная матрица X n-го порядка:

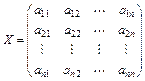. (3.6)

Представим матрицу X в виде:

, (3.7)

где

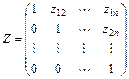, . (3.8)

Известно, что определитель матрицы равен произведению определителей:

, (3.9)

но 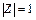, поэтому

. (3.10)

Формулы для вычисления элементов матриц 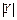и получаются перемножением матриц 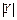, и приравниванием к соответствующим элементам матрицы X:

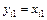; , при (3.11)

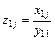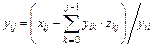; , при 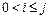. (3.12)

Ниже приводится листинг файла Determinant.m, содержащий описание функции, возвращающей значение определителя матрицы, вычисляемого в соответствие с (3.11), (3.12).

% листинг файла Determinant.m

function Z=Determinant(A)

P=1;

C=0;

N=size(A,1);

y=zeros(N);

z=zeros(N);

for i=1:N

y(i,1)=A(i,1);

z(i,i)=1;

End;

for j=2:N

z(1,j)=A(1,j)/y(1,1);

End;

for i=2:N

for j=2:N

if (j>=2)&(j<=i)

s=0;

for k=1:j-1

s=s+y(i,k)*z(k,j);

End;

y(i,j)=A(i,j)-s;

End;

if (i>1)&(i<j)

s=0;

for k=1:i-1

s=s+y(i,k)*z(k,j);

End;

z(i,j)=(A(i,j)-s)/y(i,i);

End;

End;

End;

s=1;

for i=1:N

s=s*y(i,i);

End;

Z=s;

Для вычисления определителя квадратной матрицы A, созданной в предыдущем примере, следует ввести команду

>> Determinant(A)

ans =

7.0510e+003

Для проверки правильности работы данной функции полезно сравнить результат, возвращенный функцией Determinant( ) и результат, возвращаемый функцией встроенной в пакет MATLAB:

>> det(A)

ans =