Все доказанные свойства справедливы для определителей любого порядка
Примеры. Вычислить определители.
1. 1 7 0
2 -1 -3 = 2 - 21*5 + 0 – 0 - (-3)*41 - 14*2 = 2 -105+12-28 =14-133=-119
5 4 2
2. + + +
4 6 -2 1 (-4) (- 6) (2) 0 0 0 1
1 -1 3 5 = -19 -31 13 5 19 31 13
3 -10 2 1 -1 -16 4 1 = -1 1 16 4 =
6 0 12 2 -2 -12 16 2 2 12 16
19 31 13 19 31 13 19 31 13
= -2 1 16 4 = -2 1 16 4 = -2 1 26 0 =
1 6 8 0 -10 4 0 -10 4
= -2 * (12*26*4 + 130 – 31*4) = -4 * (12*26*2 + 65 – 31*2) = -4 * (12*26*2 + 3)
Замечание. Так как всякий определитель связан с квадратной матрицей, то все доказанные свойства можно «привязать» к матрице.
Например. Если элементы двух строк квадратной матрицы равны, то определитель этой матрицы ∆ = |A|=0.
Лекция 2. Обратная матрица.
Число b называют обратным по отношению к числу a, если ab=1 В этом случае b=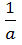 
= a-1 aa-1 ≡ 1
| Определение. Матрица В называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А слева или справа получается единичная матрица: AB=BA=E |
В этом случае для обратной матрицы В вводится обозначение В=А-1.
Из свойств определителей и условия A-1A=AA-1=Eследует
|А-1А|=| А-1||А|
| А-1|*|А|= 1, |А-1|=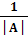 
, |А|≠ 0
|А-1А|=| Е|= 1
Очевидно, говорить о существовании обратной матрицы для матрицы А можно лишь том случае, если │А│≠ 0. В этом случае матрица Аназывается невырожденной. Если |A|=0, то матрица А называется вырожденной(особенной).
Вырожденная матрица не имеет обратной матрицы.
│А│≠ 0- необходимое и достаточное условие существования обратной матрицы.
| Теорема. Если матрица А невырожденная, то существует обратная матрица А-1 и при этом единственная, для которой справедливо равенство: А*А-1 = А-1 *А = Е |
Дата добавления: 2015-08-21; просмотров: 475;