Метод Гаусса и его реализация в пакете MATLAB

Рассмотрим систему линейных алгебраических уравнений

(3.4)

при условии, что матрица A=(a_ij) невырождена.

Метод Гаусса состоит в преобразовании системы (3.4) последовательным исключением переменных к равносильной системе с треугольной матрицей

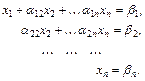(3.5)

Затем из системы (3.5) последовательно находят значения всех неизвестных .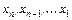

Т.о., процесс решения системы (3.4) распадается на два этапа:

1. Прямой ход - приведение системы (3.4) к треугольному виду.

2. Обратный ход - нахождение значений неизвестных переменных, в соответствие с (3.5).

Для реализации метод Гаусса в пакете MATLAB необходимо:

1. Создать файл Exchange.m, содержащий описание функции, осуществляющей перестановку строк при обнаружении в текущей строке нулевого элемента на главной диагонали.

% листинг файла Exchange.m

function z=Exchange(C,i)

k=i+1;

while C(k,i)==0

k=k+1;

End;

for j=1:size(C,1)

s=C(i,j);

C(i,j)=C(k,j);

C(k,j)=s;

End;

z=C;

2. Создание файла Simplex.m, содержащего описание функции, возвращающей расширенную матрицу системы к диагональному виду

% листинг файла Simplex.m

function z=Simplex(A,b)

N=size(A,1);% определение числа уравнений системы

C=cat(2,A,b);% создание расширенной матрицы системы

for i=1:N-1

if C(i,i)==0

C=Exchange(C,i);

End;

for j=0:N

C(i,N+1-j)=C(i,N+1-j)/C(i,i);

End;

for m=i+1:N

alpha=C(m,i);

for j=i:N+1

C(m,j)=C(m,j)-alpha*C(i,j);

End;

End;

End;

C(N,N+1)=C(N,N+1)/C(N,N);

C(N,N)=1;

z=C;

3. Создать файл Gauss.m, содержащий описание функции, возвращающей решение системы линейных уравнений методом Гаусса.

% листинг файла Gauss.m

function z=Gauss(A,b)

C=Simplex(A,b);

N=size(A,1);

v(N)=C(N,N+1);

for j=1:N-1

s=0;

for k=0:j-1

s=s+C(N-j,N-k)*v(N-k);

End;

v(N-j)=(C(N-j,N+1)-s)/C(N-j,N-j);

End;

z=v';

4. Задать матрицу системы линейных уравнений

>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]

A =

1 2 3 4 5

10 9 8 7 6

5 9 11 12 13

20 1 3 17 14

12 10 4 16 15

5. Задать вектор-столбец свободных членов

>> b=[10;20;30;40;50]

b =

10.0000

20.0000

30.0000

40.0000

50.0000

6. Решить систему уравнений, используя функцию Gauss( )

x=Gauss(A,b)

x =

0.0964

1.4324

-1.3530

1.6593

0.8921

7. Проверка правильности решения системы линейных уравнений

>> A*x

ans =

10.0000

20.0000

30.0000

40.0000

50.0000