Выражения. дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m ´ n, В – матрица размером m ´ к

Х=В’/A’

Х=В’* (А^ - 1)’

Х=В’* inv(A’)

Х=A\В

дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m ´ n, В – матрица размером m ´ к. Более сложные случаи решения систем уравнений (2) с плохо обусловленной матрицей А требуют применения специальных методов решения.

Для решения системы линейных уравнений вида

Ax=b,

где A - матрица коэффициентов при неизвестных, x - вектор-столбец неизвестных, b - вектор-столбец свободных членов, в пакете MATLAB достаточно выполнить следующую команду:

>> A^-1*b

Пример 1.

Решить систему 4-х линейных уравнений:

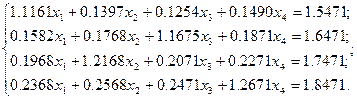
Протокол программы (в скрипт-файле)

a= [1.1161 0.1397 0.1254 0.1490 ;

0.1582 0.1768 1.1675 0.1871 ;

0.1968 1.2168 0.2071 0.2271 ;

0.2368 0.2568 0.2471 1.2671] ;

b= [1.5471 ; 1.6471 ; 1.7471 ; 1.8471] ;

Х4 = а \ b

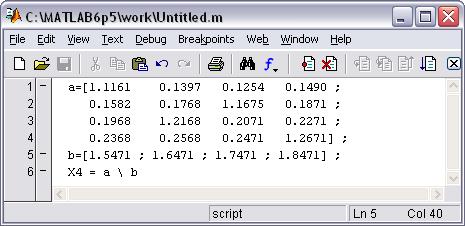
Рис.1 Скрипт-файл решения СЛАУ с помощью оператора Х=A\В

в окне редактора-отладчика

Эта программа выдает решение заданной системы с помощью четвертого оператора в виде матрицы – столбца

Х4=

1.0406

0.9351

0.9870

0.8813

X1 = b’/a’

X2 = b’*(a^-1)’

X3 = b’*inv(a’)

Результаты решения

X1 =

1.0406 0.9351 0.9870 0.8813

X2 =

1.0406 0.9351 0.9870 0.8813

X3 =

1.0406 0.9351 0.9870 0.8813

Отметим, что сравнение скорости решения системы линейных уравнений с помощью средств матричной алгебры пакета MATLAB и функции Zeidel( ), листинг которой приведен в предыдущем разделе свидетельствует о неоспоримом преимуществе первых.

Данное обстоятельство обусловлено тем, что в пакете MATLAB, который изначально разрабатывался для проведения матричных вычислений, используются специальные быстрые алгоритмы для выполнения арифметических операций с матрицами. Поэтому при решении каких-либо прикладных задач, в ходе которого возникает необходимость решения систем линейных уравнений, целесообразнее использовать встроенные возможности пакета MATLAB.