Dot(tmp,tmp)

ans =

0.0687

Можно найти решение рассмотренной выше задачи регрессии в пакете MATLAB можно другим способом. Для следует использовать тот факт, что коэффициенты искомой функции, минимизирующей сумму квадратов отклонений, являются решением переопределенной системы уравнений. Для случая интерполяции полиномом второй степени данных, приведенных выше, система уравнений имеет вид:

.

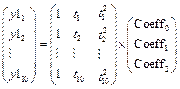Решение данной системы уравнений, удовлетворяющее методу наименьших квадратов, находится с помощью оператора \:

Coeff = A\y1,

где

,

.

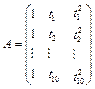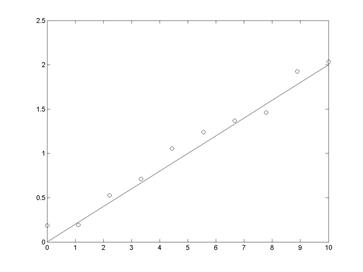
Рис. 7.2

Таким образом, альтернативный подход к нахождению коэффициентов аппроксимирующего полинома реализуются выполнением следующей последовательности команд:

>> B=[ones(size(x')) x' x'.^2]

B =

1.0000 0 0

1.0000 1.1111 1.2346

1.0000 2.2222 4.9383

1.0000 3.3333 11.1111

1.0000 4.4444 19.7531

1.0000 5.5556 30.8642

1.0000 6.6667 44.4444

1.0000 7.7778 60.4938

1.0000 8.8889 79.0123

1.0000 10.0000 100.0000

>> Coeff=B\y1

ans =

0.1049

0.1904

0.0004

Для решения системы линейных уравнений метода наименьших квадратов при использовании аппроксимации линейной комбинацией известных функций в пакете MATLAB можно использовать метод, описанный в предыдущем разделе. Ниже представлена последовательность команд, позволяющая найти коэффициенты аппроксимирующей функции вида .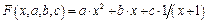

% Задание исходных данных

>> vx=[0;0.2;0.4;0.6;0.8;1]

vx =

0.2000

0.4000

0.6000

0.8000

1.0000

>> vy=[0.43;0.22;0.8;0.12;1;2]

vy =

0.4300

0.2200

0.8000

0.1200

1.0000

2.0000

% задание матрицы переопределенной системы уравнений

>> D=[vx.^2 vx 1./(vx+1)]

>> D

D =

0 0 1.0000

0.0400 0.2000 0.8333

0.1600 0.4000 0.7143

0.3600 0.6000 0.6250

0.6400 0.8000 0.5556

1.0000 1.0000 0.5000

>> Coeff=D\vy

Coeff =

3.0521

-1.4391

0.5126

% визуализация исходных данных и аппроксимирующей функции

>> i=1:length(vx);

>> j=1:length(X);

>> X=vx(1):0.01:vx(6);

>> Y=[ones(size(X')) X' X'.^2]*Coeff;% вычисление значений

% аппроксимирующей

% функции

>> plot(vx(i),vy(i),'o',X(j),Y(j))% (рис. 7.3)

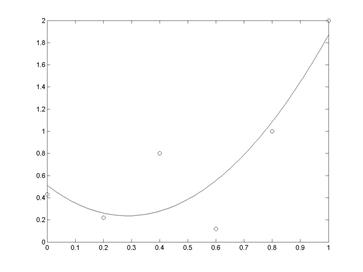
Рис. 7.3