Определение 2. Движением материальной точки в криволинейных координатах времени называем дважды непрерывно дифференцируемые функции
Движением материальной точки в криволинейных координатах времени 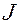 называем дважды непрерывно дифференцируемые функции
называем дважды непрерывно дифференцируемые функции  , задающие криволинейные координаты точки
, задающие криволинейные координаты точки 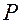 в каждый момент времени
в каждый момент времени 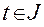 .
.
Задать движение в криволинейных координатах — это значит:
— задать зависимость положения 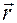 материальной точки
материальной точки 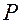 от ее криволинейных координат
от ее криволинейных координат
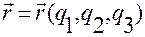 ,
,
— задать закон изменения криволинейных координат материальной точки 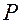 от времени на промежутке
от времени на промежутке 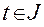
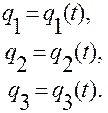
Если известно движение  материальной точки в криволинейных координатах
материальной точки в криволинейных координатах  , то векторное задание ее движения получим подстановкой функций
, то векторное задание ее движения получим подстановкой функций  в вектор-функцию
в вектор-функцию  , устанавливающую связь положения точки с криволинейными координатами:
, устанавливающую связь положения точки с криволинейными координатами:
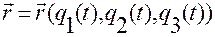 .
.
Дата добавления: 2015-08-21; просмотров: 526;
