Основная система координат
Зафиксируем точку 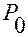 с криволинейными координатами
с криволинейными координатами 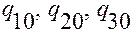 .
.
Введем следующую аффинную систему координат(см. рис.1.5.3):
· Начало ее совпадает с точкой 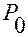 .
.
· Первая координатная ось совпадает с касательной в точке 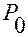 к первой координатной линии.
к первой координатной линии.
· Вторая координатная ось совпадает с касательной в точке 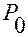 ко второй координатной линии.
ко второй координатной линии.
· Третья координатная ось совпадает с касательной в точке 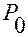 к третьей координатной линии.
к третьей координатной линии.
На рисунке 1.5.3 координатная ось с номером 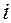 обозначена
обозначена 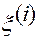 ,
, 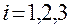 . Координатная линия с номером
. Координатная линия с номером 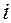 обозначена
обозначена 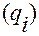 . Координатная поверхность с номером
. Координатная поверхность с номером 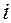 обозначена
обозначена 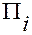 . Координатные линии выделены жирным цветом.
. Координатные линии выделены жирным цветом.
Так как  — дважды непрерывно дифференцируемая функция, то функция
— дважды непрерывно дифференцируемая функция, то функция 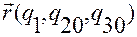 будет также дважды непрерывно дифференцируемой по
будет также дважды непрерывно дифференцируемой по 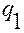 .
.
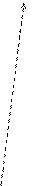
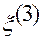

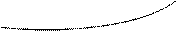

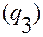
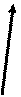


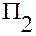
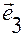
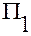
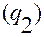


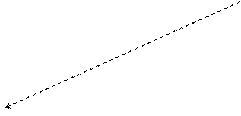




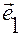
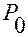
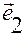

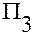
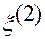
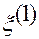
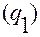
Рис. 1.5.3
Аналогичное утверждение справедливо для функции 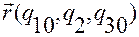 относительно
относительно 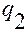 и для функции
и для функции 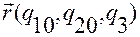 относительно
относительно 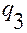 . Поэтому касательные к координатным линиям в точке
. Поэтому касательные к координатным линиям в точке 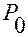 существуют.
существуют.
Направляющие векторы этих касательных будут коллинеарны, соответственно, векторам
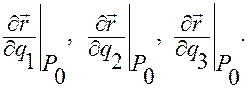
Здесь выражение 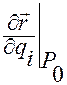 означает, что вектор
означает, что вектор 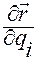 вычислен в точке
вычислен в точке 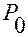 с координатами
с координатами 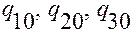 .
.
В силу условия (1.5.2):
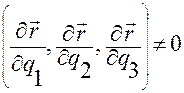 , (1.5.2)
, (1.5.2)
векторы 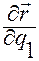 ,
, 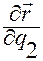 ,
, 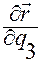 в точке
в точке 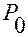 будут некомпланарными.
будут некомпланарными.
Обозначим орты этих векторов 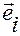 ,
, 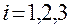 . Тогда можем записать:
. Тогда можем записать:
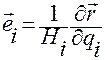 ,
, 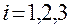 , (1.5.5)
, (1.5.5)
где
 .
.
Очевидно, вектор 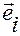 указывает направление изменения положения
указывает направление изменения положения 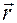 точки
точки 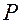 относительно точки
относительно точки 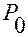 при возрастании координаты
при возрастании координаты 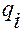 .
.
Дата добавления: 2015-08-21; просмотров: 555;
