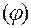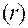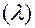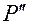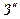Сферическая система координат

Положение точки 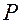задается криволинейными координатами 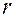, , 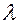, 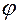которые называются сферическими (см. рис.1.5.2).

Сферические координаты имеют следующий геометрический смысл:

Координата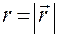 —это расстояние от полюса 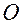декартовой прямоугольной системы координат до точки .

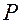Принимает значения .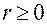

Координата 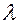— это угол в плоскости 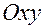между положительным направлением оси 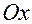и проекцией 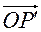вектора 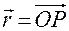на плоскость .

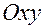Принимает значения в диапазоне .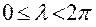

Положительное направление отсчета угла 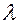задается правилом правой руки относительно орта .

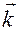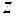
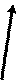
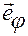
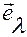
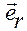
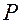
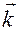
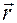
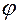
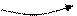
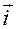
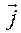
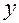
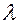
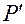
Рис. 1.5.2

Координата 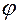— это угол между плоскостью 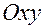и радиус-вектором 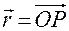точки .

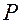Угол 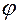отсчитывается от плоскости 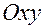до радиус-вектора .

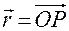Изменяться в диапазоне .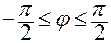

В частности, он принимает значения:

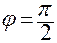— если 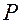находится на положительной
полуоси ;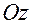

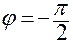— если 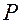находится на отрицательной
полуоси ;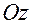

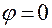— если 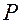находится в плоскости 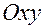и не
совпадает с точкой .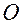

Угол 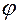положителен, если точка 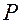принадлежит положительному полупространству 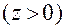относительно плоскости 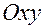; угол 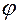отрицателен, если 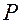находится в отрицательном полупространстве 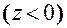относительно плоскости .

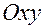На рисунке 1.5.2 точка 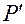обозначает ортогональную проекцию точки 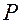на плоскость 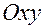, а 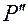— ортогональную проекцию точки 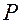на ось .

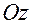Связь декартовых прямоугольных координат 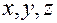точки 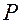со сферическимизадается формулами:

,

,

.

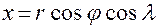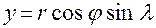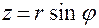Обратная зависимость, т.е. связь сферических координат с декартовыми, имеет вид:

,

,

.

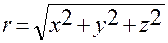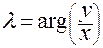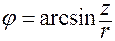Угол 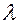не определен в том случае, когда точка 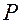находится на оси .

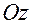Угол 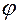не определен в том случае, когда точка 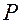совпадает с точкой .