Решение. Строим политропу с показателем n = 0,8 на фоне частных, характерных процессов в одной какой-нибудь диаграмме или в обеих p – v и T – s так

Строим политропу с показателем n = 0,8 на фоне частных, характерных процессов в одной какой-нибудь диаграмме или в обеих p – v и T – s так, как рекомендовано выше. Точку «а» располагаем на плоскости диаграммы произвольно (см. рис. 3.5).

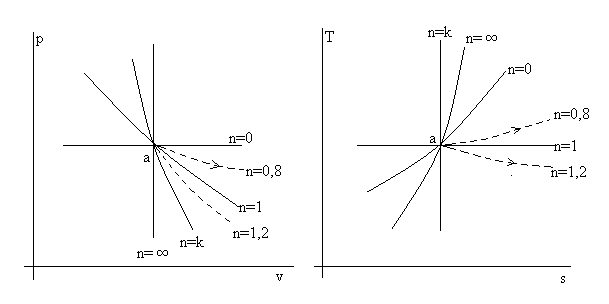
Рис. 3.5. Иллюстрация применения правила изотермы

и адиабаты при решении задачи.

1. Отмечаем, что по условию Δv > 0 (расширение). Следовательно, w > 0.
2. Глядя на рис.3.5, видно, что ΔT > 0 и Δs > 0.
3. Из условия ΔT > 0 следует, что Δu > 0 и Δh > 0 (du = c_vdT, dh = c_pdT, c_v,c_p > 0).

Из условия Δs > 0 следует, что q > 0 (dq = Tds, T > 0).

Ответ:Δu, Δh, Δs, q, w > 0, т.е. все изменения строго положительны, и качественный анализ процесса завершен.

Замечание.Если в предыдущей задаче сделать n = 1.2 и по-прежнему рассмотреть расширение газа, то ΔТ < 0, а Δs > 0. Тогда ответ задачи: Δu < 0, Δh < 0, Δs > 0, q > 0, w > 0, т.е. при росте энтропии (теплота подводится) температура уменьшается (за счет совершаемой работы над окружающей средой).

Замечание. Вся сложность применения правила изотермы и адиабаты только в грамотном расположении политропы на фоне частных политроп с n = 0, 1, k и ∞, помятуя, что k = 1,3 – 1,6 (для одно – трех атомных газов).