со свойствами реальных газов и веществ.

Эту методику продемонстрируем на конкретном примере: рассмотрим изохорный процесс v = const и рабочее вещество – Н₂О (μ = 18 кг/кмоль), а рассчитывать процесс будем дважды, сначала как для идеального газа, потом как для реального вещества.

Текст задачи.В реакторе объемом V = 0,75 м³ под давлением р₁ = 10 бар и при температуре t₁ = 180⁰С находится вода в количестве m = 3,85 кг. При подводе внешней теплоты давление поднимается до р₂ = 16 бар. Определить температуру t₂ в конце нагрева, количество подведенной теплоты и изменение энтропии.

Решение (Н₂О – идеальный газ).

1. Температура воды в реакторе в конце процесса нагрева:

v = const → T₂ / T₁ = p₂ / p₁ → T₂ = T₁p₂ / p₁ = (273 + 180)16 / 10 = 724K = 451⁰C.

2. Количество подведенной теплоты:

Q = mq = mc_v|_t1^t2(t₂ – t₁).

По таблицам теплоемкостей для водяного пара имеем:

μс_p|₀¹⁸⁰ = 34,195 кДж/кмольК, μс_p|₀⁴⁵¹ = 35,364 кДж/кмольК.

Тогда средняя изобарная массовая теплоемкость равна:

c_p|₁₈₀⁴⁵¹ = (μc_p|₀^t2t₂ – μc_p|₀^t2t₁) / μ(t₂ – t₁) = (35,364*451 – 34,195*180) / 18(451 – 180) = 1,972 кДж/кгК.

По уравнению Майера находим среднюю изохорную массовую теплоемкость:

c_v|₁₈₀⁴⁵¹ = c_p|₁₈₀⁴⁵¹ – R/μ = 1,972 – 8,314 / 18 = 1,512 кДж/кгК.

Окончательно, Q = 3,85*1,512*(451 – 180) = 1577,5 = 1580 кДж.

3. Изменение энтропии за процесс нагрева:

Δs = c_v|_t1^t2 lnT₂/T₁ = 1,512 ln (273 + 451)/(273 + 180) = 0,70897 = 0,709 кДж/кгК.

ΔS = m*Δs = 3,85*0,709 =2,73 кДж/К.

Ответ:t₂ = 451⁰C, Q = 1580 кДж, ΔS = 2,73 кДж/К.

Решение ( Н₂О – реальное вещество).

Решать будем с помощью таблиц для воды (см. фрагмент таблицы, представленный выше).

1. Начальное состояние воды. Известно, что

р₁ = 10 бар и v₁ = V/m = 0,75/3,85 = 0,1948 = 0,195 м³/кг = const.

По таблицам насыщенных паров воды (по давлениям, т.к. дано р₁ = 10 бар, см. выше фрагмент таблицы насыщенных паров воды) определяем температуру фазового перехода t_нас = 179,88⁰С. Одновременно, обращаем внимание, что v΄΄ = 0,1946 м³/кг. Получилось, что

t_нас = 179,88⁰С ≈ 180⁰С и v΄΄ = 0,1946 м³/кг ≈ v₁ = 0,195 м³/кг.

Следовательно, в начальном состоянии вода находится в состоянии сухого насыщенного пара.

2. Температура в реакторе после нагрева.

Определяем состояние воды после нагрева. При р₂ = 16 бар по той же таблице имеем v΄΄ = 0,1238 м³/кг. Но при v = const v₂ = 0,195 м³/кг. Следовательно, v΄΄ < v_2, и делаем вывод: в конце процесса нагрева вода находится в состоянии перегретого пара.

Открываем таблицу перегретого пара для воды, зная, что р₂ = 16 бар и v₂ = 0,195 м³/кг, находим величину температуры: t₂ = 416⁰C.

3. Количество подведенной теплоты в процессе нагрева реактора.

q = u₂ – u₁, т.к. v = const. u = h – pv.

u₁ = h₁ – p₁v₁ = h΄΄(p₁ = 10 бар) – p₁v₁ = 2778 – 10*10⁵*0,195*10^-3 = 2583,4 = 2580 кДж/кг.

Здесь величину h₁ = h΄΄ = 2778 кдж/кг взяли из той же таблицы насыщенного водяного пара, а v₁ = v = 0,195 м³/кг. Величина 10^-3 во втором слагаемом просто переводит размерность его в кДж/кг.

u₂ = h₂ – p₂v₂ = 3288,2 – 16*10⁵*0,195*10^-3 = 2976,8 = 2980 кДж/кг.

Здесь величину h₂ = 3288,2 кдж/кг нашли по таблице для перегретого водяного пара при р₂ = 16 бар и v₂ = 0,195 м³/кг. Отсюда

q = 2980 – 2580 = 400 кДж/кг. Q = 3,85*400 = 1540 кДж.

4.Изменение энтропии: Δs = s₂ – s₁ = s₂ – s΄΄(p₁ = 10 бар) = 7,283 – 6,587 = 0,696 кДж/кгК.

ΔS = m*Δs = 3,85*0,696 = 2,6796 = 2,68 кДж/К.

Ответ:t₂ = 416⁰C, Q = 1540 кДж, ΔS = 2,68 кДж/К.

Сравнивая ответы решения одной и той же задачи для водяного пара как идеального газа и как реального вещества, видно, что погрешность расчета Q и ΔS находится в нормальных пределах (2 – 3)%, как это принято в химической технологии. Зато погрешность определения температуры t₂ великовата:

δt₂ = Δt₂/t₂ = (451 – 416)/416*100% = 8,4%.

На рис. 3.8 приведена иллюстрация решения задачи двумя способами.

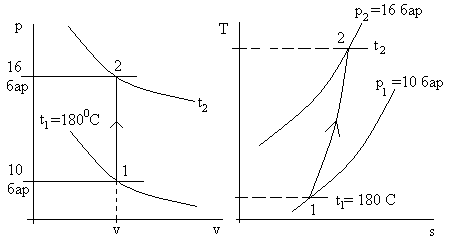
Рис. 3.8а. Изображение процесса в рассмотренной задаче

в осях р – v и T – s. H₂O – идеальный газ. Величины Т₂, q ,Δs – искомые.

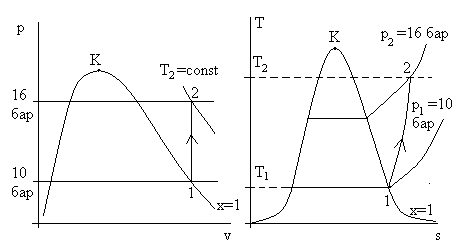
Рис. 3.8б. Изображение процесса в рассмотренной задаче

в осях p – v и T – s. H₂O – реальное вещество. Величины Т₂, q, Δs – искомые.

Замечание.Методика расчета процессов с реальными веществами по таблицам кажется сложной только в том, что сначала надо определить фазовое состояние вещества в начальной и конечной точке процесса, а потом уже пользоваться соответствующими таблицами для поиска необходимых термодинамических величин. Использование фазовых диаграмм для расчета процессов вообще трудностей не представляет, хотя точность расчета меньше, чем при пользовании таблиц.