Уравнение процесса.

В лекции 2 довольно кратко уже говорилось о политропе, теперь – подробнее.

Уравнение политропического процесса имеет вид:

pvⁿ = const, n = const.

Но это не единственная форма связи параметров состояния, возможны комбинации:

pT^n΄ = const, n΄ = const или vT^n΄΄= const, n΄΄= const.

Далее, для примера, будем работать с уравнением pvⁿ = const, n = const.

На практике показатель политропы n находят экспериментально следующим образом:

pvⁿ = const → lnp + nlnv = const → lnp = - nlnv + const.

Последнее выражение представляет собой уравнение прямой линии в координатах lnp – lnv. В эксперименте с каким-то веществом для различных условий измеряют давление р и удельный объем v с какой-то инструментальной точностью. Далее строят график в осях lnp – lnv (см. рис. 3. 1) и по нему находят показатель политропы n.

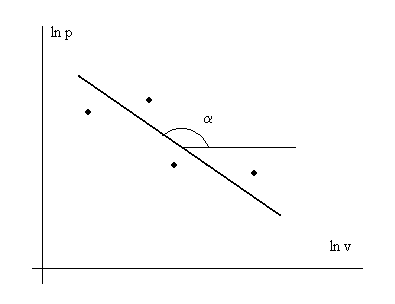
Рис. 3. 1. Иллюстрация к экспериментальному определению

показателя политропы n – индикаторная диаграмма

в логарифмических координатах. n = - tgα.

· - обозначение экспериментальных точек.

Истоки вывода уравнения pvⁿ = const уходят в анализ работы реальных поршневых машин (паровых и компрессоров). При анализе их работы снимали индикаторную диаграмму p = f(x), где х – ход поршня. От индикаторной диаграммы всего один шаг до p – v диаграммы.

Показатель политропы n в уравнении pvⁿ = const в сущности отражает интенсивность изменения параметров в процессе, т.е. характер смены состояний. А параметры изменяются под влиянием внешних воздействий q и w на термодеформационную систему. Поэтому мы в праве ожидать, что n = n(q,w). Проверим это ожидание.

Исходное уравнение политропы pvⁿ = const в логарифмической форме

lnp = -nlnv + const

после дифференцирования принимает вид:

dp/p = -n dv/v или n = -vdp/pdv (3.1)

Иными словами: показатель политропы n есть отношение элементарной работы проталкивания к элементарной работе деформации (сжатия или расширения), и наши ожидания подтвердились.

Далее, вспомним первый закон термодинамики в форме

du = dq – dw → du = dq – pdv → pdv = dq – du; (3.2.1)

dh = dq +dw΄ → dh = dq +vdp → vdp = dh – dq; (3.2.2)

Подстановка (3.2.1) и (3.2.2) в (3.1) дает результат:

n = (dq – dh) / (dq –du). (3.3)

В лекции 2 подробно рассматривалось понятие теплоемкости и было показано, что dq = cdT. Одновременно, для идеального газа и любого процессабыли получены связи

du = c_vdT и dh = c_pdT.

Тогда зависимость (3.3) для идеального газа принимает вид:

n = (cdT – c_pdT) / (cdT – c_vdT) = (c – c_p)/(c – c_v). (3.4)

Следовательно, показатель политропы n для идеального газа получил вполне определенный смысл – это функция теплоемкостей.

Из (3.4) попутно получим зависимость истинной политропной теплоемкости с_n от показателя политропы n , чтобы можно было рассчитывать количество теплоты так, как это принято в калориметрии dq = c_ndT. Действительно (см. (3.4)),

c ≡ c_n = (nc_v –c_p) / (n – 1) = c_v (n – k) / (n – 1). (3.5)

В (3.5) величина k ≡ с_р/с_v носит название коэффициента Пуассона и является показателем адиабаты. Для двухатомных газов k ≈ 1,4. Так как n = const и k = const, то (3.5) справедливо и для средней политропной теплоемкости:

c_n|_t1^t2 = c_v|_t1^t2(n – k) / (n – 1), k = c_p|_t1^t2 / c_v|_t1^t2. (3.6)