Частные политропные процессы.

Если какой-то параметр состояния при взаимодействии с внешней средой фиксировать, то процесс, входящий в гамму политропных, называют частным:

pvⁿ = const и p = const → n = 0 – изобарный,

а для идеального газа из (3.8) T₁/T₂ = v₁/v₂.

pvⁿ = const иv = const→ n = ± ∞ - изохорный,

а для идеального газа из (3.8) T₁/T₂ = p₁/p₂.

pvⁿ = const и T = const – изотермический,

а для идеального газа n = 1 и из (3.8) v₂/v₁ = p₁/p₂.

При s = const→ n = k ≡ c_p / c_v – изоэнтропийный (адиабатный) с уравнением

pv^k = const.

Замечание.Условие Q (q) = 0 (нет источников теплоты) означает, что Tds ≡ 0 и s = const и по первому признаку процесс назван адиабатным (adiabatos – непереходимая – в смысле тепловой изоляции)

На рис.3.2 представлены графики политроп с различными показателями n для частных процессов, только еще раз напомним, что величина показателя адиабаты для двухатомных газов k ≈ 1,4.

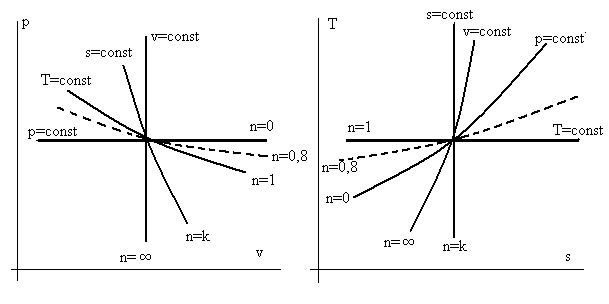
Рис. 3.2. Взаимное расположение частных политропных

процессов в осях p – v и T – s при различных значениях

показателей политропы n.

Замечание. Если необходимо построить график оригинального политропного процесса, т.е. не совпадающего с указанными частными, то, зная величину n , не сложно построить этот график на фоне частных процессов.

Пример.Построить график политропного процесса с показателем политропы n = 0,8 в осях p – v и T – s.

Решение этой задачи основано на том обстоятельстве, что линии частных процессов делят всю плоскость с координатными осями на сектора. Следовательно, график (в осях p – v или T – s) политропного процесса с каким-то n должен проходить в соответствующем секторе. На рис. 3.2 линия с n = 0,8 расположена в секторе между политропами n = 0 и n = 1 и обозначена пунктиром.

1.3. Расчет изменения функций состояния Δu, Δh