Физический смысл волновой функции

Говоря о волнах де Бройля мы говорим, что интенсивность этих волн пропорциональна вероятности обнаружить частицу в данном месте. Там, где интенсивность максимальна, там и вероятность имеет наибольшее значение.

Интенсивность волн пропорциональна квадрату амплитуды. В простейшем случае монохроматической волны ( 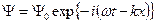) интенсивность пропорциональна квадрату амплитуды .

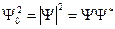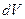Величина называется плотностью вероятности. Вероятность обнаружить частицу в объеме равна 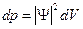. Вероятность найти частицу в конечном объем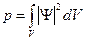е: , где 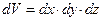. Вероятность найти частицу во всем пространстве: 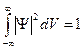- достоверная вероятность. Где-то в пространстве частица есть. Последние выражение называется условием нормировки.

Волновая функция 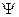описывает поведение конкретной реальной физической системы, поэтому ее математические свойства должны удовлетворять определенным физическим условиям:

1. Волновая функция должна быть однозначной и конечной. Это следует из физического смысла .
2. должна быть интегрируема. Интеграл имеет смысл вероятности, иначе условие нормировки не выполнится.
3. Волновая функция должна быть непрерывна и иметь непрерывные частные производные (состояние системы меняется непрерывно).

Волновая функция, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние 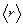электрона от ядра вычисляют по формуле:

Лекция 12
Атом водорода в квантовой механике