Уравнение Шредингера. Волновая функция.

Обнаружение волновых свойств микрочастиц свидетельствовало о том, что классическая механика не может правильно описать их поведение. Шредингером, Гейзенбергом, и Дираком была создана квантовая механика или волновая механика. Квантовая механика способна объяснить поведение микрочастиц. Она дает вероятностный характер описания явлений. Основным уравнением квантовой механики является уравнение Шредингера. Подобно тому, как законы Ньютона не выводятся, а является обобщением большого числа опытных фактов, так и уравнение Шредингера не выводятся. Оно постулируется. Шредингер записал уравнение, основываясь на экспериментальных результатах.

Состояние микрочастиц в квантовой механике описывается волновой функцией 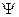. Она является функцией координат и времени и может быть найдена из уравнения Шредингера:

.

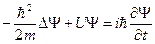Это временное уравнение Шредингера для случая, когда 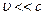. Здесь 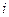- мнимая единица ( 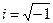), , 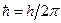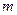- масса частицы, 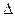- оператор Лапласа ( 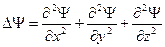), 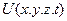- потенциальная энергия частицы.

Вид волновой функции определяется видом потенциала 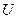, а следовательно, характером сил, действующих на частицу.

Дирак обобщил это уравнение для больших скоростей ( 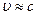) и создал релятивискую квантовую механику.

Если потенциальная энергия частиц 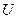не зависит от времени явно, то решение уравнения Шредингера можно представить в виде произведения двух функций, одна из которых функция координат, а другая – времени ( 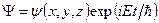). В этом случае координатная волновая функция 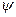удовлетворяет стационарному уравнению Шредингера:

,

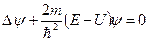где - полная энергия частиц, постоянная, в случае стационарного поля.

Функции 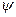, удовлетворяющие этому уравнению при заданном виде 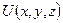, называют собственными. Они существуют лишь при определенных значениях , называемых собственными значениями энергии. Собственные значения могут образовывать как сплошной спектр, так и дискретный. Отыскание собственных значений энергии и собственных функций составляет важнейшую задачу квантовой механики.