Соотношение неопределенностей Гейзенберга

В классической механике каждая частица движется по определенной траектории, то есть в любой момент времени она имеет определенную координату и импульс. Микрочастицы из-за наличия у них волновых свойств существенно отличаются от классических частиц. Одно из основных различий заключается в том, что нельзя говорить о движении частиц по определенной траектории, то есть нельзя одновременно точно определить значение координаты и импульса.

Для того, чтобы рассмотреть эту важнейшую особенность микрочастиц будем исходить из явления их дифракции. Согласно гипотезе де Бройля 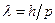. Слева стоит длина волны, но она не является функцией координат. Выражение «длина волны в точке равна 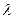» - бессмысленно, но так как импульс выражается через длину волны, то он тоже не должен зависеть от координаты. Отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. 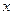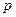Выражение «импульс частицы в точке равен » в квантовой механике не имеет смысла.

Положение, что микрочастица не имеет одновременно вполне точные значения координаты и импульса выражено в соотношение неопределенностей Гейзенберга:

.

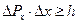Из соотношения неопределенностей следует, что если микрочастица находится в состоянии с точным значением координаты ( 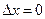), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ( 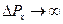), и наоборот.

Соотношение неопределенностей Гейзенберга можно пояснить на примере дифракции электронов. Пусть поток электронов проходит через узкую щель шириной 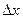, расположенную перпендикулярно направлению их движения (рис. 1).

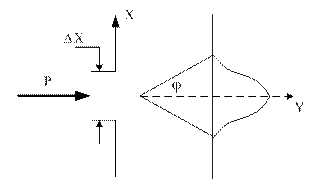Рис.1.

Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля для электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране, характеризуется главным максимумом, расположенным симметрично оси 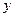, и побочными максимумами по обе стороны от главного (мы их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).

До прохождения через щель электроны двигались вдоль оси 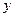, поэтому составляющая импульса , так что 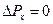, а координата 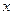частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направлении оси 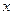определяется с точностью до ширины щели, то есть с точностью 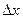. В тот же момент вследствие дифракции электроны отклоняются от первоначального направления, и будут двигаться в пределах угла 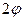. Появляется неопределенность в значении составляющей импульса вдоль оси 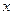, которая равна, как следует из рис.1.:

.

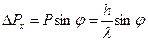Условие максимума при дифракции на щели , для первого минимума 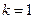, 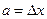. То есть

.

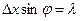Из этих формул получим:

.

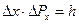Если учесть, что часть электронов попадает за предела главного максимума, то величина 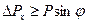, то есть

.

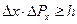Соотношение неопределенностей верно для любых движущихся тел, но для макроскопических тел длина волны де Бройля 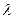ничтожно мала и не играет роли, и соотношение неопределенностей тоже несущественно. Можно говорить об одновременных значениях 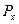и 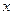, а следовательно, о траектории. Так как 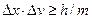, то если 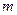велико 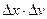мало (частицы большой массы – классические частицы).