Квантовые числа. Собственные функции , являющиеся решениями уравнения Шредингера зависят от трех квантовых чисел:
Собственные функции 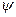 , являющиеся решениями уравнения Шредингера зависят от трех квантовых чисел:
, являющиеся решениями уравнения Шредингера зависят от трех квантовых чисел: 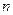 ,
, 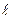 и
и 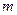 .
. 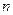 - главное квантовое число, определяет энергетические уровни электрона в атоме и принимает значения
- главное квантовое число, определяет энергетические уровни электрона в атоме и принимает значения 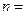 1, 2, 3,…
1, 2, 3,…
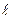 - орбитальное квантовое число, оно связано с квантованием момента импульса электрона (механического орбитального момента). То есть орбитальный момент не может быть произвольным, а принимает дискретные значения, определяемые формулой:
- орбитальное квантовое число, оно связано с квантованием момента импульса электрона (механического орбитального момента). То есть орбитальный момент не может быть произвольным, а принимает дискретные значения, определяемые формулой:
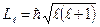
| (4) |
При данном значении 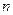
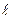 - принимает значения
- принимает значения
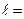 0,1, 2,…, 0,1, 2,…, 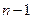 . .
|
Всего 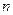 значений.
значений.
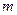 - магнитное квантовое число, связанное с квантованием проекции момента импульса на выбранное направление (обычно в направлении магнитного поля по оси
- магнитное квантовое число, связанное с квантованием проекции момента импульса на выбранное направление (обычно в направлении магнитного поля по оси 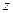 ):
):
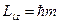
| (5) |
Магнитное квантовое число может принимать следующие значения:
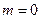 , , 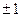 , , 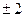 ,…, ,…, 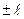
|
Всего 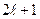 значений.
значений.
Таким образом, вектор момента импульса электрона может иметь такие ориентации в пространстве, при которых его проекция на выделенное направление (ось 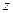 ) принимает квантованные значения согласно формуле (5). Это означает, что в магнитном поле уровень с орбитальным квантовым числом
) принимает квантованные значения согласно формуле (5). Это означает, что в магнитном поле уровень с орбитальным квантовым числом 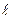 расщепляется на
расщепляется на 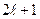 подуровней. Это было в 1896 году экспериментально обнаружено голландским физиком Зееманом.
подуровней. Это было в 1896 году экспериментально обнаружено голландским физиком Зееманом.
Из формулы (3) следует, что каждому значению 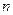 соответствует энергия
соответствует энергия 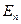 . Каждой энергии
. Каждой энергии 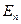 соответствует несколько волновых функций
соответствует несколько волновых функций  отличающихся значениями
отличающихся значениями 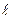 и
и 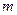 . То есть при одном и том же значении энергии атом водорода может быть в нескольких различных состояниях. Найдем число состояний с одинаковой энергией
. То есть при одном и том же значении энергии атом водорода может быть в нескольких различных состояниях. Найдем число состояний с одинаковой энергией 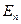 . Так как при данном
. Так как при данном 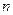 орбитальное квантовое число
орбитальное квантовое число 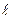 изменяется от
изменяется от 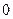 до
до 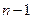 , а каждому
, а каждому 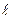 соответствует
соответствует 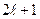 значений
значений 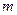 , то число различных состояний равно:
, то число различных состояний равно:
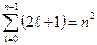
| (6) |
В квантовой механике состояния с различными 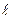 обозначают буквенными символами как и спектроскопии:
обозначают буквенными символами как и спектроскопии:
 - s-состояние
- s-состояние
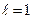 - p-состояние
- p-состояние
 - d-состояние
- d-состояние
 - f-состояние
- f-состояние
При записи квантового состояния сначала пишут численное значение 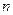 , а затем буквенное
, а затем буквенное 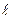 . Например, состояние
. Например, состояние 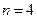 и
и  обозначают
обозначают 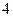 f.
f.
Квадрат модуля волновой функции 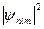 определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы «размазан», образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках атома.
определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы «размазан», образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках атома.
Квантовые числа 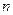 и
и 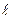 характеризуют размер и форму электронного облака, а квантовое число
характеризуют размер и форму электронного облака, а квантовое число 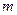 - его ориентацию в пространстве. На рис.2. для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при
- его ориентацию в пространстве. На рис.2. для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при 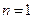 и
и 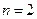 . Как видно из рисунка, оно зависит от
. Как видно из рисунка, оно зависит от 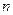 ,
, 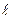 и
и 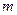 . При
. При  электронное облако имеет форму шара, при
электронное облако имеет форму шара, при 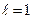 - форму гантели.
- форму гантели.
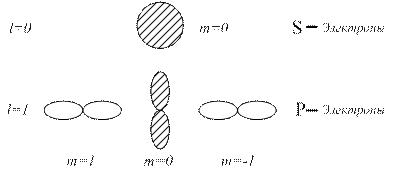 Рис.2.
Рис.2.
|
Радиус шара в 1s состоянии равен радиусу первой орбиты Бора. По теории Бора электрон может находиться только на орбите, в квантовой механике – в любом месте пространства, но с разной плотностью.
Дата добавления: 2015-08-21; просмотров: 889;
