Устойчивость АТС

Устойчивость – это совокупность свойств АТС противостоять дейст­вию возму­щающих сил, вызванных взаимодействием колес с неровно­стями дороги, аэродинами­ческими силами, наклоном дороги и др. Хорошей устойчивостью должны обладать все АТС, поскольку это свойство наряду с другими в значительной степени определяет безопасность движения.

Потеря устойчивости выражается в скольжении колес или опроки­дывании авто­мобиля. В зависимости от направления скольжения или оп­рокидывания различают про­дольную и поперечную устойчивость. Более вероятно и опасно нарушение попе­речной устойчивости.

Параметрами поперечной устойчивости могут являться:

- критические скорости кругового движения с заданным радиусом, соответст­вующие началу бокового скольжения колес или опрокидыванию АТС;

- критические углы косогора при прямолинейном движении, соот­ветствующие началу бокового скольжения или опрокидыванию;

- коэффициент поперечной устойчивости.

Кроме указанных оценочных параметров могут использоваться и другие, по­скольку общепринятая система оценочных показателей устой­чивости отсутствует.

4.6.1. Поперечная устойчивость по условиям бокового скольже­ния колес

Нарушение поперечной ус­тойчивости чаще всего возникает под действием попе­речной состав­ляющей силы инерции Р_иу cos β, либо поперечной составляющей силы тя­же­сти G_a sin β при наличии поперечного угла наклона дороги β.

На колеса действуют реакции: ∑R_zн – нор­мальные на наружные по отношению к центру по­ворота ко­леса, ∑R_zв – на внутренние, ∑R_yн, ∑R_yв – поперечные, соответственно на наружные и внут­ренние колеса.

Из условия равновесия поперечных сил и ре­акций дороги можно за­писать:

Р_иу cos β – G_a sin β = ∑R_y,

где ∑R_y = ∑R_yн + ∑R_yв.

При боковом скольжении колес сумма боковых реакций равна силе сцепления колес в поперечном направлении:

∑R_y = ∑R_z φ_y = (G_a cos β + Р_иу sin β) j_y,

где φ_y – поперечный коэффициент сцепления.

Если АТС движется равномерно по траектории радиусом R, то по­перечная сила инерции равна Р_иу = (М_a V_a²) / R.

Тогда, критическую по боковому скольжению колес скорость дви­жения можно определить из выражения:

V_кр.j = .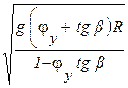

На горизонтальной дороге β = 0, и тогда

V_кр.j = .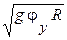

При прямолинейном движении АТС по косогору сила инерции Р_иу = 0, и скольже­ние колес в поперечном направлении вызывается соответствующей силой веса G_а sin β. Критический угол косогора по бо­ковому скольжению определяется тогда из выражения:

tg β_кр.φ = φ_y.

Наибольшее влияние на критическую скорость по боковому сколь­жению оказы­вают продольные реакции на колесах. Чем больше эти реак­ции, тем существеннее сни­жается способность колес сопротивляться боко­вому скольжению.

Если задние колеса ведущие, то сила тяги на них значительно больше, чем сила сопротивления качению передних ведомых колес. По­этому задние колеса менее ус­той­чивы при действии боковых сил, и в этом случае зачастую возникает занос (попе­речное скольжение задних колес), который также характеризует потерю устойчивости. Боковое скольжение передних колес (снос), даже если они ведущие, менее вероятно, чем занос.

4.6.2. Поперечная устойчивость по условиям бокового опроки­дывания

При действии на АТС боковых сил при определенных условиях мо­жет наступить опрокидывание относительно опоры наружных колес. Во избежание бокового опро­ки­дывания необходимо, чтобы суммы нормаль­ных реакций, действующих на левые и пра­вые колеса АТС, в отдельности удовлетворяли условию:

∑R_{z н.} ≥ 0; ∑R_{z в.} ≥ 0.

Достижение равенства нулю реакций внутренних колес свидетель­ствует о крити­ческих условиях по боковому опрокидыванию. В этом слу­чае опрокидывающий мо­мент боковых сил равен восстанавливающему моменту силы тяжести.

Если пренебречь боковым креном кузова, вызванным деформацией шин и упру­гих элементов подвески, то при движении на вираже это равен­ство запишется в виде:

(P_uy cos β – G_a sin β) h_g = (P_uy sin β + G_a cos β) 0,5 В.

При равномерном движении по траектории радиусом R критическая по условиям опрокидывания скорость движения будет равна:

V_кр.оп = .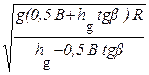

На горизонтальной дороге β = 0, и тогда:

V_кр.оп = .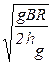

При прямолинейном движении по косогору P_uy = 0, и опрокидыва­ние может про­изойти под действием силы G_a sin β. В этом случае критический угол косогора по опро­кидыванию может быть найден из выражения:

tg β_кр.оп. = - В / 2 h_g.

Знак « - « здесь говорит о том, что опрокидывание направлено в сто­рону действия силы G_a sin β, а не Р_иу cos β, как в предыдущем случае.

Из вышеприведенных формул следует, что наличие виража увеличи­вает критиче­ские скорости по скольжению и опрокидыванию.