Постановка задачи синтеза.

В соответствии с (67) передаточная функция проектируемой системы, представленной на рис. 27, при f = s = 0 равна

. (99)

Характеристический многочлен замкнутой системы определяется как

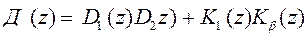. (100)

Пусть известны передаточные функции 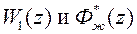,а также выбран характеристический многочлен наблюдателя 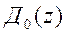. Требуется найти такое допустимое управление, которое обеспечивает равенство передаточных функций проектируемой и желаемой систем, т.е.

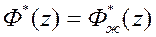. (101)

Наблюдатель с передаточной функцией 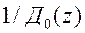можно ввести, умножая числитель и знаменатель передаточной функции желаемой системы на :

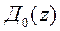. (102)

При нулевых начальных условиях динамика системы с передаточной функцией 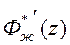не отличается от динамики желаемой системы. Однако характеристический многочлен системы с передаточной функцией 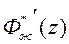будет равен

.

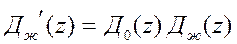Если выбрать 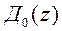так, чтобы наблюдатель был устойчивым и малоинерционным, то поведение систем с передаточными функциям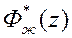и и 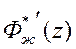будет мало отличаться и при ненулевых начальных условиях, да и то лишь в начальный этап переходного процесса.

С учетом (100), (93) из (102) получаем

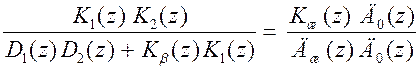. (103)

Следовательно, задача проектирования сводится к выбору многочленов 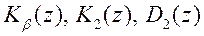, удовлетворяющих соотношению (103) и условиям допустимости управления. При этом выбором 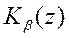и 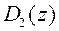обеспечивается желаемое расположение полюсов, а выбором 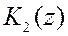- желаемое расположение нулей проектируемой системы.