Цифровой (дискретный) ЛКР-регулятор

Кроме того, возможно определение коэффициентов 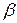для цифрового ЛКР-регулятора, исходя из квадратичного критерия качества

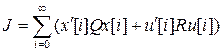, (2а)

где Q и R симметричные неотрицательно определенные весовые матрицы.

Матрица Q определяет стоимость штрафа, назначаемого за отклонение переменных состояния относительно их знчений в состоянии равновесия. Матрица R определяет стоимость штрафа, наначаемого за величину (уровень) управляющего воздействия. Эти матрицы устанавливаются пректировщиком системы. Цель управления принудить переменные состояния быть как можно ближе к нулю, в то время как штрафуется управляющее воздействие.

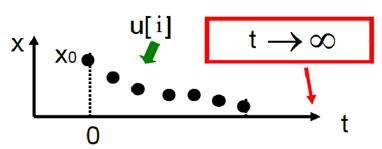
Итак, задача цифрового ЛКР управления заключается в том, чтобы найти такое управление u[i] (см. рис. ниже), которое минимизирует критерий качества 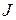при условии, что объект управления описыватся уравнением

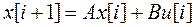
и задано начальное состояние .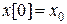

Оптимальное решение представляет собой обатную связь по состоянию

,

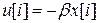где векторный коэффициент обратной связи по состоянию имеет вид

.

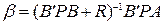В последнем выражении матрица P является решением линейного алгебраического разностного уравнения

.

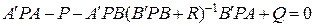При этом замкнутая система независимо от выбора весовых матриц является устойчивой, т.е. все собственные значения матрицы замкнутой системы 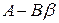имеют модули, меньшие единицы и значение оптиального критерия качества равно 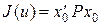. Итак, 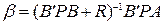минимизирует

.

Пример.

При объектах высокого порядка для определения P и 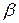целесообразно применить команду dlqr системы MATLAB.