Восстановление свойств замкнутой системы.
Можно «восстановить» свойство робастности для ЛК системы в случае минимально-фазового объекта путем процедуры, называемой восстановление свойств системы (ВСС). На английском языке эта процедура звучит как loop transfer recovery (LTR). Суть процедуры – сократить нули объекта с помощью полюсов фильтра, тогда другие полюсы могут быть взяты достаточно удаленными от мнимой оси (достаточно «быстрыми»).
Концепция ВСС заключается в следующем:
- Проектируется ЛКГ регулятор для реального объекта и шума датчика,
- Затем добавляется шум объекта и дисперсия этого шума постепенно увеличиваетя, при этом происходит настройка наблюдателя,
- При добавленном шуме ЛКГ регулятор становится более робастным, изменяя запасы устойчивости системы.
Однако, разумеется, такой ЛКГ регулятор не является оптимальным для «фактического»» уровня шума объекта.
Остановимся на процедуре ВСС более подробно. Рассмотрим структуру непрерывной оптимальной системы, применимую как для ЛК, та и для ЛКГ управления. Для ЛК управления 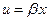 и передаточная фукция зазомнутой системы имеет вид
и передаточная фукция зазомнутой системы имеет вид
 .
.
При этом, как уже сказано выше, получаем желаемые робастные свойства (запасы устойчивости по модулю и фазе).

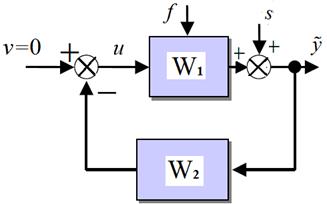
Для ЛКГ управления 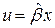 и передаточная функция разомкнутой системы
и передаточная функция разомкнутой системы
 .
.
Можно показать, что последняя передаточная функция приближается к передаточной функции разомкнутой системы при «идеальном» ЛК управлении, если 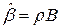 и
и 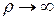 . Одним из путей добиться такого приближения свойств системы с ЛКГ управлением к свойствам системы с ЛК управлением заменить f
. Одним из путей добиться такого приближения свойств системы с ЛКГ управлением к свойствам системы с ЛК управлением заменить f
на 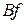 (т.е. предположить, что шум объекта аддитивен по отношению к управляющему воздействию) и положить
(т.е. предположить, что шум объекта аддитивен по отношению к управляющему воздействию) и положить 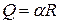 . При увеличении
. При увеличении 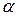 уровень шума объекта возрастает и параметр оптимального наблюдателя стремится к
уровень шума объекта возрастает и параметр оптимального наблюдателя стремится к 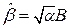 . Преимущество рассмотренного подхода состоит в том, что его применение гарантирует устойчивость наблюдателя для любого
. Преимущество рассмотренного подхода состоит в том, что его применение гарантирует устойчивость наблюдателя для любого 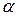 .
.

Дата добавления: 2015-08-14; просмотров: 879;
