Пространство состояний.
Свойства систем, поведение которых описывают уравнения (1) - (4), можно интерпретировать графически в ортогональном пространстве размерности n. Такое пространство, координатами которого являются переменные состояния х, называется пространством состояний.
Рассмотрим, как представляется в пространстве состояний поведение системы (1)
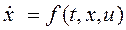 ,
,
при условии, что u = const. Для системы второго порядка
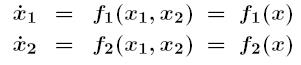
Состоянию системы в произвольный момент времени соответствует конкретная точка пространства состояний 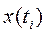 , которая называется изображающей точкой системы (рис. 1). С изменением времени эта точка выписывает траекторию, называемую фазовой траекторией системы.
, которая называется изображающей точкой системы (рис. 1). С изменением времени эта точка выписывает траекторию, называемую фазовой траекторией системы.
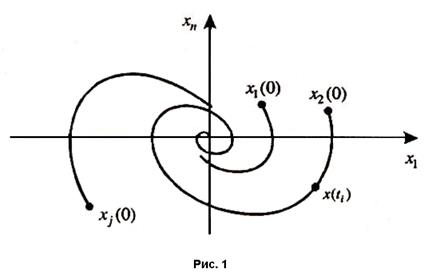
Совокупность фазовых траекторий, полученных при движении из различных начальных состояний, называют фазовым портретом системы. Он позволяет оценить свойства нелинейной системы.
 В каждый момент времени изображающая точка системы
В каждый момент времени изображающая точка системы 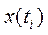 имеет определенную скорость
имеет определенную скорость 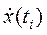 , которую также можно изобразить в пространстве состояний в виде вектора скорости, имеющего определенное направление. Совокупность векторов скорости будем называть векторным полем системы (рис. 2.). Для системы втого порядка
, которую также можно изобразить в пространстве состояний в виде вектора скорости, имеющего определенное направление. Совокупность векторов скорости будем называть векторным полем системы (рис. 2.). Для системы втого порядка
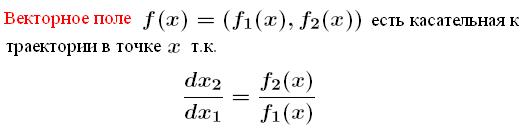
Точки пространства состояний, в которых вектор скорости равен нулю
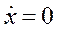 , (5)
, (5)
представляют собой точки или состояния равновесия (особые точки) системы.
Пример. Маятник при M =0 описываются уравнениями
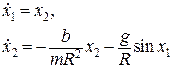

Отметим, что в пространстве состояний можно также исследовать свойства линейных систем, рассмотренных в предыдущих разделах.

Пример. Для системы, описываемой уравнениями
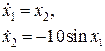
векторное поле выглядит, как показано на рис. ниже
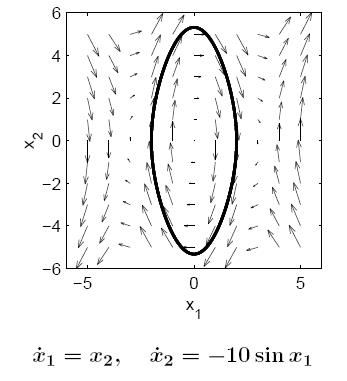
Дата добавления: 2015-08-14; просмотров: 1025;
