Опустить

Из частотных критериев остановимся кратко на критерии Найквиста применительно к цифровой системе с единичной обратной связью (с одной степенью свободы).

Рассмотрим два случая применения критерия Найквиста.

1. Разомкнутая цифровая система устойчивая. Такая система является устойчивой, если все полюсы ее передаточной функции 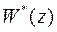расположены внутри окружности единичного радиуса. При этом система не включает в себя дискретных интеграторов и, следовательно, на основании (70) 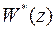можно записать в виде

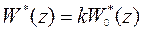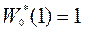, , (85)

где k- безразмерный коэффициент усиления. Полагая

,

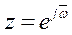в (87), получаем амплитудно-фазовую характеристику разомкнутой цифровой системы

, .

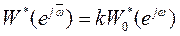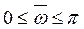Очевидно, при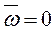

,

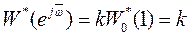т.е. АФХ разомкнутой системы начинается из точки 0 абсциссой k, расположенной на вещественной оси. С учетом того, что 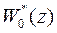есть рациональная функция z, при 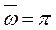получаем

.

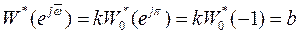Обычно 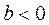. Таким образом, в отличие от непрерывных систем амплитудно-фазовая характеристика разомкнутой цифровой системы заканчивается не в начале координат, а в точке с абсциссой 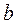, расположенной на вещественной оси.

Аналог критерия Найквиста гласит: если разомкнутая цифровая cиcтема устойчивая, то для устойчивости замкнутой цифровой системы необходимо и достаточно, чтобы АФХ разомкнутой цифровой системы 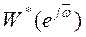при изменении 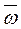от 0 до 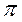не охватывала критическую точку с координатами

(-1; j0). В качестве примера рассмотрим амплитудно-фазовые характеристики двух устойчивых разомкнутых цифровых систем (Рис.24).

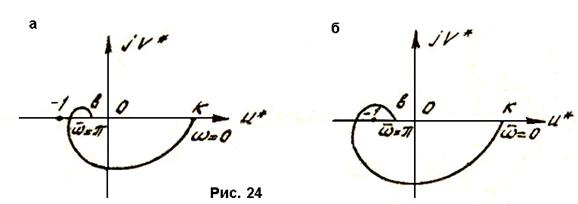
Согласно аналогу критерия Найквиста, в случае "а" замкнутая цифровая система также устойчивая, а в случае "б" она является неустойчивой.

2. Разомкнутая цифровая система является нейтрально устойчивой. При этом ее передаточная функция имеет вид

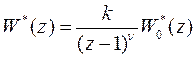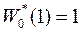, . (70)

Здесь 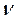определяет число дискретных интеграторов, входящих в функцию 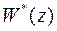, а функция 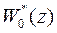содержат все полюсы внутри окружности единичного радиуса. При 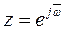получаем выражение для амплитудно-фазовой характеристики разомкнутой цифровой системы

.

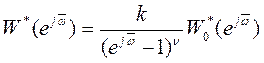Отсюда нетрудно показать, что при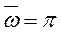

,

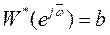где b- вещественное число, а при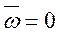

, .

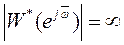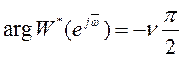Следовательно, АФХ разомкнутой нейтрально устойчивой цифровой системы начинается либо на вещественной (при четных 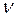) либо на мнимой оси (при нечетных 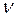) в бесконечно удаленной от начала координат точке, а заканчивается на вещественной оси.

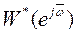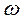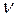Аналог критерия Найквиста, являющийся по существу модификацией критерия Найквиста непрерывных систем, гласит: если разомкнутая ЦСАУ является нейтрально устойчивой, то для устойчивости замкнутой цифровой системы необходимо и достаточно, чтобы АФХ разомкнутой цифровой системы при изменении от 0 до , дополненная дугой бесконечно большого радиуса в четвертей окружности, не охватывала точки с координатами ( 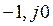), где 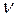- число единичных полюсов разомкнутой цифровой системы. На рис 25 приведены две амплитудно-фазовые характеристики разомкнутой цифровой системы для .

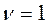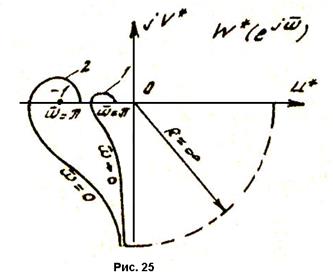Годограф 1, дополненный дугой в четверть окружности бесконечно большого радиуса R, не охватывает точки ( 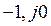). При этом замкнутая цифровая система является устойчивой. Для годографа 2 аналог критерия устойчивости не выполняется, что свидетельствует о неустойчивости замкнутой цифровой системы.

Лекция