Уравнения цифровой системы с обратной связью.
Уравнениями цифровой системы с обратной связью называют линейные разностные уравнения, связывающие управляемую y[i]и управляющую u[i] последовательности с внешними последовательностями - задающей V[i], возмущающей f[i] и шума измерений s[i]. Для получения таких уравнений удобно воспользоваться структурной схемой, приведенной на рис. 23.
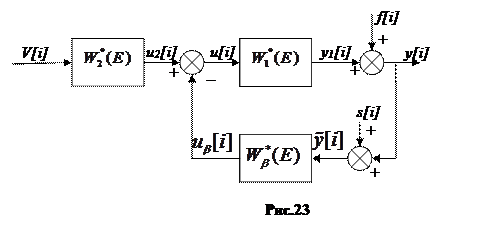
Так как представленная на этом рисунке схема соответствует линейной системе, для которой справедлив принцип суперпозиции, то Z-изображение управляемой последовательности можно найти как сумму Z-изображений реакций системы на каждую из внешних последовательностей в отдельности. При этом, учитывая определения основных передаточных функций цифровой системы с обратной связью, т.е. принимая во внимание выражения (67-68, 71-74), получаем
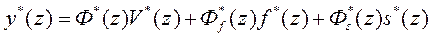 , (76)
, (76)
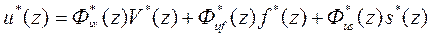 , (77)
, (77)
Передаточные функций прямой 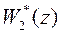 и обратной
и обратной 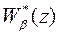 связи, дискретная передаточная функция объекта управления
связи, дискретная передаточная функция объекта управления 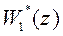 , как соответствующие дискретным фильтрам, представляют собой отношение многочленов от z:
, как соответствующие дискретным фильтрам, представляют собой отношение многочленов от z:
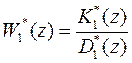 ,
, 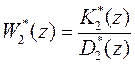 ,
, 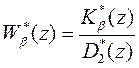 . (78)
. (78)
Знаменатели передаточных функций 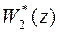 и
и 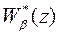 при формировании закона управления выбираются одинаковыми, что позволяет упростить процедуру синтеза.
при формировании закона управления выбираются одинаковыми, что позволяет упростить процедуру синтеза.
Подставляя (78) в (67),(68) и (71-74), находим передаточные функции замкнутой системы также в виде отношения многочленов:
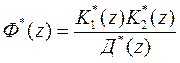 ,
,  ,
, 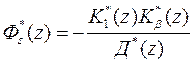 , (79)
, (79)
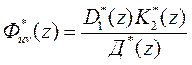 ,
, 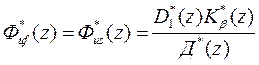 ,
,
где
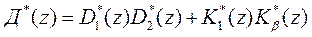 ,
,
представляет собой характеристический многочлен цифровой системы управления с обратной связью.
Для системы n-го порядка этот многочлен можно преобразовать к виду
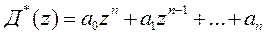 , (80)
, (80)
где al, 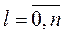 - постоянные коэффициенты.
- постоянные коэффициенты.
Как видим, сигналы в системе с прямой и обратной связью (с двумя степенями свободы) характеризуются шестью передаточными функциями (иногда называемыми «бандой шести»).
Особого внимания заслуживают функция чувствительности и дополнительная функция чувствительности.
Система с единичной обратной связью (с одной степенью свободы) описывается четырьмя передаточными функциями (банда четырех).
Подставляя (79) в (80)и умножая затем левую и правую части полученного выражения Д*(z), находим уравнения цифровой системы с обратной связью в изображениях относительно у*(z):
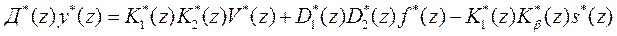 . (81)
. (81)
Заменяя в выражениях для многочленов z на оператор сдвига E и записывая вместо Z-изображений соответствующие последовательности, получаем уравнение цифровой системы с обратной связью в операторной форме
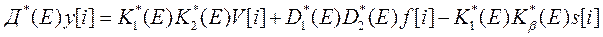 . (82)
. (82)
При известных операторных многочленах нетрудно перейти, используя свойства оператора сдвига, к явной форме линейного разностного уравнения цифровой системы с обратной связью.
Если все внешние воздействия отсутствуют, т.е. если
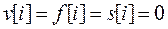 ,
,
то уравнение (81) вырождается в однородное разностное уравнение
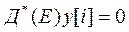 .
.
Дата добавления: 2015-08-14; просмотров: 946;
