Исходные данные. 1. Считается известной передаточная функция объекта, управляемого от ЦВМ, другими словами, дискретная передаточная функция объекта управления

1. Считается известной передаточная функция объекта, управляемого от ЦВМ, другими словами, дискретная передаточная функция объекта управления

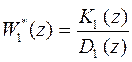, (95)

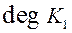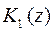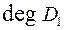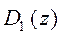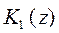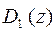где степень многочлена меньше степени многочлена . Кроме того, предположим, что многочлены и не имеют общих сомножителей, и что многочлен 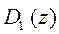является приведенным, т.е. коэффициент при старшем члене равен единице. Для упрощения записи многочлены от z будем обозначать без звездочки. Способ определения передаточной функции 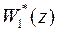по передаточной функции 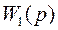непрерывного объекта был описан ранее (см. формулу (30)).

2. Задана также желаемая передаточная функция

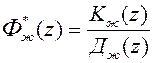, (96)

связывающая выход 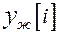устойчивой желаемой системы с задающей последовательностью v[i], причем

= ,

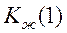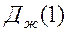так что в установившемся режиме постоянная единичная задающая последовательность воспроизводится точно. Для упрощения записи многочлены от z будем обозначать без звездочки. Методика выбора ПФ желаемой системы приведена на с.22 методических указаний 2291.

В рассматриваемом методе возмущения, к которым относят возмущающее воздействие f[i], приведенное к входу объекта, шум измерений s[i], неопределенность и изменение передаточной функции объекта управления (ошибки моделирования) учитываются косвенно путем введения ограничений на многочлен наблюдателя 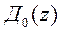, о котором будет сказано ниже, а также путем введения допустимого управления. При этом прежде всего, надо решить вопрос о форме закона управления. Здесь возможны варианты, например закон управления по ошибке, комбинация закона по ошибке с внутренней (местной) обратной связью и т.п.

3. Ограничимся рассмотрением закона управления, который в изображениях имеет вид

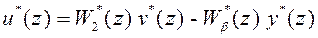, (97)

где, как и прежде [см. рис. 27 и формулы (61) и (62)], передаточные функции

,

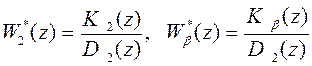определяют свойства управляющего устройства.

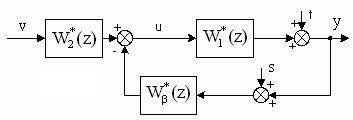
Рис. 27

4.Задаются условия допустимости управления:

а) физическая осуществимость. Условия

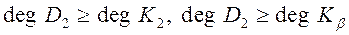, (98)

гарантируют, что алгоритмы управления, определяемые передаточными функциям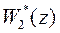и и 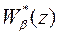, физически осуществимы;

б) возмущения f и s и изменение параметров объекта управления. Передаточная функция 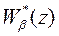обратной связи является допустимой, если она позволяет в достаточной степени ослабить влияние на управляемую величину возмущающего воздействия f, шума измерения s, а также неточности задания или изменения в процессе работы математической модели объекта управления. Закон управления, обеспечивающий качественное поведение системы при изменениях параметров объекта, приводит к робастному управляющему устройству (от английского слова "robust", что означает крепкий, сильный, грубый).

Вводя в функцию 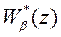дискретный интегратор, т.е. выбирая знаменатель этой функции в виде

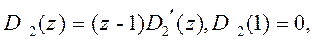
так что ПФ по возмущению Ф(1)=0, можно исключить влияние постоянного возмущающего воздействия на управляемую величину в установившемся режиме. При этом отклонение управляемой величины, вызванное низкочастотным возмущением, будет также небольшим, так как значения амплитудно-частотной характеристики обратной связи 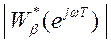на этих частотах будут велики. Кроме того, введение интегратора обеспечивает малую чувствительность (робастность) проектируемой системы к неопределенности и изменениям передаточной функции объекта управления, влияющим на прохождение низкочастотных сигналов. Высокочастотные возмущающие воздействия подавляются самим объектом управления, являющимся, как правило, с точки зрения его частотных свойств фильтром низких частот.

Влияние высокочастотных шумов измерений на управляемую величину можно ослабить, если выбрать 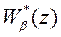так, чтобы амплитудно-частотная характеристика разомкнутого контура 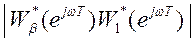быстро спадала с увеличением частоты. В области высоких частот АЧХ, связывающая управляющий сигнал и шум измерения,

= .

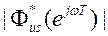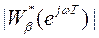Поэтому в плане предотвращения больших значений управляющего сигнала, обусловленных шумом измерения, надо обеспечить приемлемые значения АЧХ обратной связи на высоких частотах.