Опустить. Рассмотрим систему (48), полагая, что

Рассмотрим систему (48), полагая, что 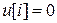. При этом общность решения не страдает, поскольку при известном 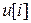всегда можно найти 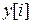. Допустим, что измерены . Тогда можно записать следующую систему из nl уравнений:

,

,

…

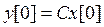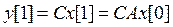с n неизвестными 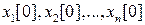, являющимися компонентами вектора 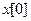. Как и прежде, полагаем размерность вектора 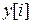равной l.

Используя векторно-матричную форму записи, получаем

.

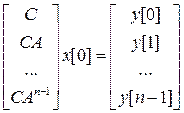Вектор состояния 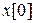можно найти из этого уравнения тогда и только тогда, когда матрица наблюдаемости размерностью ( )

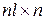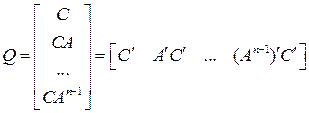(49)

имеет ранг n.

Читать

Теорема. Цифровая система n-порядка (48) наблюдаема тогда и только тогда, когда матрица наблюдаемости размерностью ( )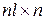

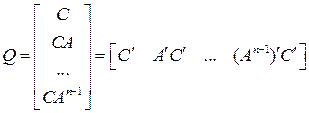(49)

имеет ранг n.

Для системы с одним выходом l=1 матрица Q является квадратной размерностью ( 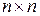), -при этом условии наблюдаемости принимает вид

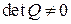. (50)

По своей сути наблюдаемость требует, чтобы каждая переменная состояния оказывала влияние на управляемую величину.