Частотные свойства цифровой системы.

Многие мощные методы анализа и синтеза систем управления базируются на частотных характеристиках. При этом основная идея заключается в том, чтобы использовать тот факт, что линейная стационарная система полностью описывается своей установившейся реакцией на гармонические сигналы. Частотные характеристики особенно полезны при исследовании робастности. Надо отметить, что свойства частотных характеристик цифровых систем значительно сложнее, чем непрерывных. Причина заключается в периодической дискретизации, операции, присущей цифровым системам. Мы вначале остановимся на дискретизации непрерывного гармонического сигнала, а затем кратко обсудим частотные характеристики цифровых систем.

Поглощение частоты. Пусть непрерывный гармонический сигнал

,

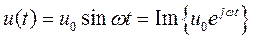с векторной амплитудой 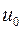и частотой 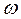подвергается дискретизации. Полагая

t=iT, (здесь Т- период дискретизации), получаем гармоническую последовательность

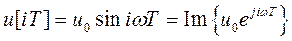. (51)

В силу того, что

,

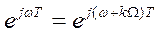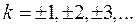
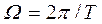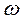
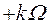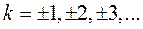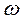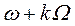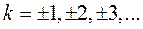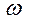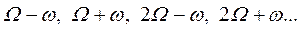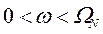где - частота дискретизации, все гармонические сигналы с частотами , , в результате дискретизации дают одну и ту же гармоническую последовательность (51). Следовательно, можно считать, что частота поглощает частоты , . Принято рассматривать только положительные частоты, поэтому частота поглощает частоты непрерывного сигнала , где . Здесь частота Найквиста 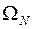определяется как половина частоты дискретизации:

.

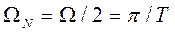В результате частота 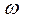неотделима от своих скрытых, или поглощенных частот.

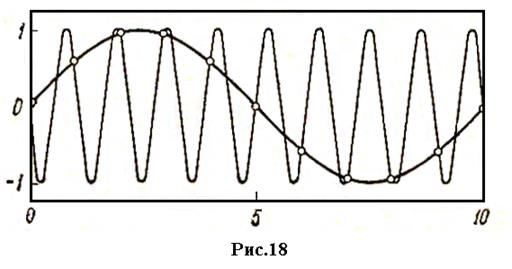
Заметим, что хотя дискретизация является линейной операцией, она зависит от времени. Этим объясняется, почему при дискретизации возникают новые частоты. Эффект поглощения иллюстрируется на рис. 18: два непрерывных гармонических сигнала с частотой 0,1 Гц и 0,9 Гц, подвергаются дискретизации с частотой 1 Гц (Т=1с). Видно, что оба сигнала в моменты дискретизации имеют одинаковые значения.

Пусть непрерывный сигнал u(t) с частотой 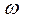, рад/с подвергается дискретизации с частотой 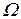, рад/с.

Показано, что, если частота непрерывного сигнала 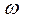больше, чем 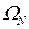, то имеет место поглощения частоты, в результате чего получается дискретный сигнал 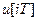с частотой 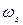, которая меньше частоты 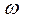. Рис. ниже показывает связь между частотам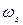и и .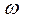

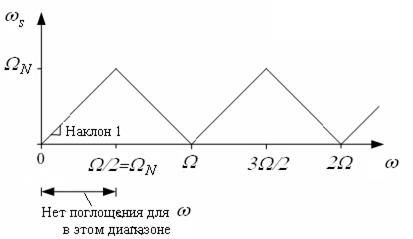
Из этого рисунка следует, что частота 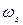равна разности 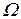- 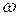, если частота 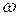лежит между частотам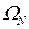и и 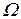. Если частота непрерывного сигнала 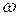меньше, чем 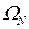, то никакого поглощения частот не наблюдается.

Для рассмотренного выше примера для f _N = 0.5 гц при f=0.1гц частота f_s =0.1гц, т.к. f< f _N. Однако при f=0.9гц частота f_s = 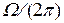- f =(1-0.9)гц =0.1гц, т.к. 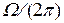>f > f _N .