Опустить. Эту теорему можно доказать следующим образом

Эту теорему можно доказать следующим образом. Если цифровая система при i=0 находилась в начале координат ( 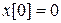),то согласно (13)

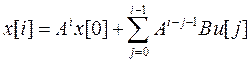(13)

состояние системы в момент времени 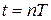определяется соотношением

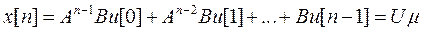, (46)

где матраца U определяется выражением (45), а

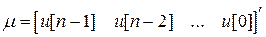
представляет собой составной вектор размерностью 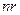. В развёрнутой форме векторно-матричное уравнение (46) есть не что иное, как система n скалярных уравнений с 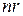неизвестными 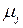, , 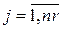являющимися компонентами вектора 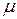. Подобная система совместна, т.е. существует хотя бы одно решение, которое обращает в тождества все уравнения, входящие в (46), если ранг матрицы U равен n. Заметим, что такое решение не единственно, если существует более одного входного сигнала, т.е. если r>1.

Для системы с одним входом (r=1) размерность матрицы U равна 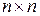. При этом условие управляемости принимает вид

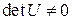. (47)

Пример. Для двойного интегратора, управляемого от ЦВМ, матрицы А и В определяются выражениями

. .

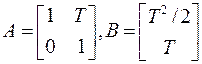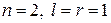В этой случае матрица управляемости

,

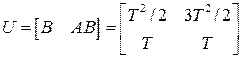так что

, .

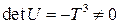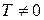Следовательно, цифровая система с двойным интегратором полностью управляема, если 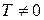. Заметим, что по своей сути полная управляемость требует, чтобы каждая переменная состояния была чувствительной к управляющему сигналу.