Алгоритм построения модели

Наиболее известная модель функционирования рынка основана на теории общего равновесия. Модель общего равновесия проявляется в механизме действия фондовых бирж, где аукционист сравнивает спрос и предложение участников рынка и, повышая или снижая цены, регулирует куплю-продажу. Рассмотрим имитацию действия рыночного механизма с помощью модели общего равновесия Эрроу-Гурвица.

В качестве хозяйственных субъектов, участвующих в процессе функционирования рынка, выберем два предприятия, каждое из которых, располагая одним доступным им обоим ресурсом (например, трудом), производит по одному виду продукции конечного спроса, и одного потребителя, предъявляющего этот спрос. Условимся также, что обмен осуществляется через единственного посредника – аукциониста. В этом случае экономический цикл будет выглядеть так (рис. 55):

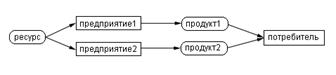
Рис. 55 – Схема экономического цикла

Проблема оптимального распределения ресурсов для такой экономики формулируется следующим образом:

Условия спроса и предложения продукции:

Y_i^s= F_i(L_i^d)≥Y_i^d.

Условия спроса и предложения ресурсов:

L₁^d+L₂^d ≤L^s.

Функция полезности, максимизируемая потребителем:

U(Y₁^d,Y₂^d)→max.

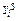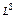Здесь объем предложения i-го продукта i-м предприятием; объем спроса со стороны потребителя на i-й продукт; предложение ресурса (постоянная величина); 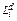объем спроса на ресурс со стороны i-го предприятия; 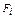производственная функция i-го предприятия; U – функция полезности потребителя.

Рыночный процесс по Вальрасу (модель Эрроу-Гурвица) – это постепенное приближение к решению описанной задачи путем итеративного диалога (обмена информацией) между участниками процесса.

Рассмотрим алгоритм решения этой задачи, где каждая итерация t будет состоять из приведенных ниже четырех шагов процесса регуляции рынка.

1. Аукционист указывает i-му предприятию цену на его продукцию P_i(t) и цену ресурса W(t), а также сообщает потребителю цены P_i (t) и цену спроса, равную предельной полезности 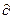U/ 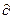Y_i^d(t-1), где i=1,2.

2. i-e предприятие, исходя из заданных ему цен, выбирает такое сочетание затрат и результатов производства (L_i^d(t), Y_i^s(t)), которое максимизирует его прибыль π_i(t) = P_i(t)*F_i(L_i^d(t))-W_i(t)*L_i^d(t), и представляет это сочетание на рассмотрение аукциониста.

3. Потребитель предъявляет спрос на i-й продукт следующим образом. Если на i-й продукт спроса нет или если предельная полезность потребления меньше предельных затрат, то потребитель оставляет величину спроса без изменений. В противном случае он корректирует спрос пропорционально разнице между предельной полезностью и предельными затратами и в результате указывает соответствующую величину Y_i^d(t ) (рис. 56).

4. Аукционист, руководствуясь законом спроса и предложения, изменяет цены. Если спрос на продукт превышает предложение, он поднимает цену и наоборот. Однако в том случае, если избыточный спрос отрицателен и соответствующие ему цены равны нулю, снизить цены ниже существующего уровня невозможно (что, в частности, следует и из блок-схемы рассматриваемого нами процесса).

Производственная функция и функция полезности определяются следующим образом:

Y_i^s = c_i*(L_i^d)^a_i (a_i<1), U = b₁*Ln Y₁^d + b₂*Ln Y₂^d.

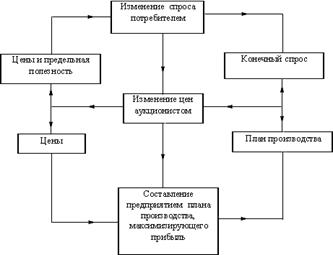
Рис. 56 - Блок-схема модели Эрроу-Гурвица