Накопление капитала
Современный экономический рост – это, в определении С. Кузнеца, экономическое развитие, при котором долгосрочные темпы роста производства устойчиво превышают темпы роста населения.
Темп роста производства – это темп роста валового внутреннего продукта (ВВП). Основной показатель экономического роста – темп прироста производства ВВП на душу населения.
Модель экономического роста разработал Р. Солоу. Он рассматривал три фактора экономического роста: накопление капитала; рост народонаселения; научно-технический прогресс (НТП).
Эти факторы вводятся в анализ последовательно. Сначала рассматривается влияние на экономический рост накопления капитала при стабильном населении и неизменных технологиях и технике. Затем к накоплению капитала добавляется рост народонаселения, и, наконец к первым двум факторам добавляется НТП.
В основу анализа положена производственная функция вида Y=F(K, L), где Y – валовой внутренний продукт (ВВП), К – капитал, L – труд. Чтобы на первом этапе анализа исключить учет роста народонаселения, Y, K и L делят на L:
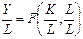 .
.
Вводятся обозначения:
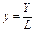 – ВВП на единицу труда или производительность труда;
– ВВП на единицу труда или производительность труда;
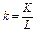 – капиталовооруженность труда, т.е. количество капитала, приходящееся на единицу труда.
– капиталовооруженность труда, т.е. количество капитала, приходящееся на единицу труда.
В результате получается производственная функция:
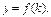
На рис. 57 показан вид этой функции.
 y
y

y=f(k)
x
Рис. 57 – Зависимость производительности труда
от капиталовооруженности
Под предельной производительностью капитала понимается прирост производительности в результате прироста капиталовооруженности на единицу. Пусть 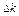 – прирост капиталовооруженности,
– прирост капиталовооруженности, 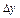 – прирост производительности в результате прироста капиталовооруженности, my – предельная производительность капиталовооруженности. Тогда:
– прирост производительности в результате прироста капиталовооруженности, my – предельная производительность капиталовооруженности. Тогда:
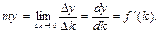
ВВП на душу населения y используется на потребление и накопление (инвестиции): y = c+ i, где c – потребление; i – накопление; s – норма накопления;
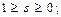
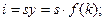
c = y – i = y – sy = (1 – s)y;
(1 – s) – норма потребления.
Накопленный капитал амортизируется (изнашивается). В экономической практике обычно принимается, что амортизация линейно зависит от количества капитала. Обозначим: а – амортизация; 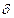 – норма амортизации, тогда
– норма амортизации, тогда 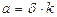 .
.
Обозначим: 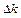 – прирост капиталовооруженности. Накопление i идет на валовые инвестиции, т.е. на возмещение амортизации а и прирост капитала (чистые инвестиции), который обозначим
– прирост капиталовооруженности. Накопление i идет на валовые инвестиции, т.е. на возмещение амортизации а и прирост капитала (чистые инвестиции), который обозначим 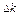 = i-a.
= i-a.
Как видно на рисунке 58, с ростом капиталовооруженности при фиксированной норме накопления наступает момент, когда прирост капитала прекращается: 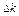 =0.
=0.
 y, a, i
y, a, i
 y=f(k)
y=f(k)

 c*
c*
|
|


i*
 k* k
k* k
Рис. 58 – Влияние капиталовооруженности на амортизацию,
инвестиции и производительность труда
В точке пересечения графиков инвестиций и амортизации выполняется условие i =a или 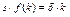 . В этой точке прирост капитала прекращается и возникает состояние устойчивого уровня накопления капитала, который обозначим k*. В этой точке k=k*=const,..
. В этой точке прирост капитала прекращается и возникает состояние устойчивого уровня накопления капитала, который обозначим k*. В этой точке k=k*=const,.. 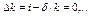 i=i*=cosnt,.. c=c*=cosnt Р.Солоу делает важнейший вывод: невозможно обеспечить непрерывный экономический рост только за счет накопления капитала. Увеличив норму накопления s, можно увеличить накопление капитала k и объем производства y. Но все равно наступит устойчивый уровень накопления капитала при крайне низком потреблении. Большая часть произведенного продукта будет тратиться на возмещение износа капитала.
i=i*=cosnt,.. c=c*=cosnt Р.Солоу делает важнейший вывод: невозможно обеспечить непрерывный экономический рост только за счет накопления капитала. Увеличив норму накопления s, можно увеличить накопление капитала k и объем производства y. Но все равно наступит устойчивый уровень накопления капитала при крайне низком потреблении. Большая часть произведенного продукта будет тратиться на возмещение износа капитала.
Возникает проблема поиска нормы накопления, приводящей к наибольшему устойчивому потреблению. Устойчивое потребление существует тогда, когда инвестиции равны амортизации, т.е. 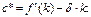 Найдем максимум c*, взяв производную от c* как функции k, и приравняв ее нулю:
Найдем максимум c*, взяв производную от c* как функции k, и приравняв ее нулю: 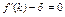 или
или 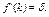
Решение этого уравнения дает значение k, при котором возникает наибольшее устойчивое потребление. Этот уровень Солоу назвал золотым. На рисунке 59 показано графическое решение задачи.
 i
i
|
|




|
|
 k** k
k** k
Рис. 59 – Графическое решение задачи определения нормы накопления
для наиболее устойчивого потребления
Условие 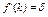 означает, что эта касательная параллельна графику амортизации
означает, что эта касательная параллельна графику амортизации 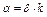 . Точку касания обозначим М. Из точки М опустим вертикаль, которая пересечется с графиком амортизации в точке N. Через эту точку должен проходить график
. Точку касания обозначим М. Из точки М опустим вертикаль, которая пересечется с графиком амортизации в точке N. Через эту точку должен проходить график 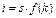 . Две звездочки при величинах k, y, i, s, c означают, что они относятся к золотому уровню. Золотой уровень накопления капитала определяется решением уравнения
. Две звездочки при величинах k, y, i, s, c означают, что они относятся к золотому уровню. Золотой уровень накопления капитала определяется решением уравнения 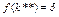 . Значения остальных величин вычисляются по формулам:
. Значения остальных величин вычисляются по формулам:
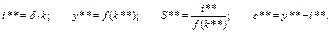
Дата добавления: 2015-08-14; просмотров: 778;
