Экономико-статистическое моделирование

Каждая производственная функция описывается одним из перечисленных алгебраических уравнений, поэтому основная задача исследования состоит в том, чтобы в каждом отдельном случае подобрать такое уравнение, которое наиболее близко воспроизводило бы исследуемый экономический процесс или его отдельные стороны. Этот этап исследования называется экономико-статистическим моделированием.

Построению математической модели производственной функции должен предшествовать тщательный качественный анализ модели­руемого экономического процесса. Только после теоретического анализа и выявления характера взаимосвязей между рассматривае­мыми признаками можно уверенно и с пользой применять производ­ственные функции для изучения экономических процессов.

Экономико-статистическое моделирование осуществляется в сле­дующем порядке:

1) экономический анализ, определение зависимой переменной и выявление факторов, влияющих на ее значение;

2) получение статистических данных и их обработка;

3) определение математической формы связи независимых и зависимой переменных (вида алгебраического уравнения);

4) определение параметров экономико-математической модели;

5) статистическая и экономическая оценка модели;

6) экономическая интерпретация модели.

Зависимую переменную выбирают на основе логического анализа возможных взаимосвязей между признаками, формирующими данный экономический процесс. За зависимую переменную принимается такой показатель, который, исходя из поставленной задачи иссле­дования, наиболее полно характеризует изучаемый экономический процесс. Он должен быть качественно четко сформулирован и вы­ражен в конкретной мере. При его выборе необходимо учитывать факторы времени и пространства. Зависимая переменная может быть выражена с помощью прямого показателя, непосредственно характе­ризующего результат производства (урожайность культур, продуктивность животных), и какого-либо косвенного показателя (себе­стоимость, рентабельность, прибыль).

Весьма важно правильно отобрать независимые факторы, влияю­щие на результат производства. В сложном переплетении явлений экономической жизни практически невозможно учесть влияние всех факторов. Значение многих из них нам неизвестно, как неизвестна и мера их влияния на результат. Не все факторы поддаются точному измерению. Часть из них оказывает незначительное влияние, неко­торые имеют субъективный характер, то есть зависят от коллектива данного хозяйства и уровня руководства производством. В зависи­мости от цели исследования необходимо из всего множества отби­рать только такие количественно измеримые факторы, которые ока­зывают наиболее существенное влияние на изменение производствен­ного результата. Влияние же второстепенных и субъективных факторов в процессе определения производственных функций усред­няется.

Число отобранных факторов не должно быть слишком большим даже в том случае, когда они известны и могут быть выражены количественно, поскольку это усложняет модель и повышает трудоемкость ее решения. Включаемые в модель факторы не должны находиться между собой в функциональной связи, так как они будут характеризовать одну и ту же сторону изучаемого явления, косвенно дублировать друг друга. В модель нельзя включать факторы, один из которых является частью другого.

После определения зависимой и независимых переменных гото­вят исходную информацию, которая должна наполнить живым со­держанием модель производственной функции. Под подготовкой исходной информации обычно понимают получение данных и их об­работку. Применяют два основных метода информации: получение исходных данных экспериментальным путем и путем обработки ста­тистических данных. Эти методы часто взаимно дополняют друг друга.

Экспериментальный способ подготовки данных имеет то преиму­щество, что информация получается в результате опыта, условия которого позволяют контролировать процесс получения данных. Экспериментатор имеет возможность непосредственно контролиро­вать большое количество переменных и тем самым сокращать то их число, которое не может быть охвачено наблюдением. Одновремен­но он по своему усмотрению может установить уровень воздействия тех или иных факторов, в результате чего прийти к решению, какую конкретную комбинацию факторов ему следует изучить. Используя эту возможность, он может добиться устранения ошибок наблюдения. Весьма важно и то, что экспериментатор может выбрать такую ком­бинацию факторов, которая даст равномерное распределение наблю­дений на той части производственной поверхности, которую необ­ходимо изучить.

Однако проведение экономического эксперимента связано со значительными трудностями. Часто оно нарушает нормальный ход производственного процесса и вызывает материальные потери. Кро­ме того, экономический эксперимент требует больших затрат време­ни, труда и средств, а во многих случаях его проведение вообще не­возможно. В этих случаях производственные функции определяют на основе информации, полученной статистическим путем. Статисти­ческие данные обычно берут из материалов отчетности сельскохо­зяйственных предприятий. Они отражают события после их сверше­ния, поэтому не могут подвергаться контролю и преобразованию в процессе их подготовки. Однако достоверная информация, содер­жащаяся в статистических данных, отражает объективную реаль­ность хозяйственной деятельности и имеет большую практическую ценность.

Статистические данные должны отвечать ряду требований. Во-первых, достаточно большой объем выборки, чтобы полученные ре­зультаты с заданной вероятностью достоверно характеризовали бы генеральную совокупность; во-вторых, однородность выборки, то есть исходные данные должны отражать наиболее типичные черты изучаемой генеральной совокупности и, в-третьих, количественное выражение исходных данных, то есть каждый фактор измеряется однозначно некоторым числом или системой чисел.

Исходные статистические данные должны быть достаточными по количеству. Опыт показывает, что практически для расчетов необ­ходимо иметь не менее 20-30 наблюдений. При использовании та­ких совокупностей известную пользу могут принести специально разработанные в математической статистике приемы малой выборки. Если единиц наблюдений мало, то для расширения исследуемой со­вокупности можно использовать так называемый метод хозяйства-лет. Суть его заключается в том, что по каждому хозяйству, входя­щему в совокупность, берут данные за ряд лет и рассматривают их как данные отдельного хозяйства. Однако этот метод не всегда дает положительные результаты.

Один из самых сложных и ответственных этапов экономико-ста­тистического моделирования - установление математической фор­мы связи между переменными изучаемого экономического процесса в виде алгебраического уравнения. Геометрическим образом этого уравнения будет прямая или кривая какого-то типа при парной кор­реляции, многомерное пространство при множественной кор­реляции. Во всех случаях необходимо, чтобы ферма этого уравне­ния, с одной стороны, правильно отражала основную тенденцию связи между переменными, а с другой - поддавалась дальнейшей математической обработке, не была слишком сложной.

Теория экономико-статистического моделирования не дает ни­каких советов относительно выбора конкретного вида алгебраиче­ского уравнения производственной функции. В практике исследова­ния существует два подхода к решению этого вопроса. Первый способ сводится к сравнительно произвольному подбору вида уравнения, более или менее соответствующего поставленной задаче исследова­ния. При этом уравнение подбирают обычно на основе графического анализа соотношений между переменными. Однако если моделируе­мых переменных больше трех, их общее взаимодействие графически изобразить уже невозможно. Второй способ предполагает, что вы­бор вида уравнения необходимо, прежде всего, строго экономически обосновать.

При построении многих производственных функций не всегда требуется выбирать соответствующий вид уравнений. Можно с успе­хом использовать типовые модели, построенные при предыдущих исследованиях подобных зависимостей. Построенную модель про­изводственной функции необходимо решить, то есть вычислить чис­ловые значения ее параметров. Вычисление параметров производится обычно с помощью метода наименьших квадратов.

О практической ценности производственной функции можно су­дить только после оценки полученных результатов. При оценке адек­ватности (соответствия) полученной модели действительным взаимо­связям между факторами используют коэффициенты корреляции и корреляционного отношения. Для вычисления этих показателей существует ряд расчетных формул, являющихся модификациями основных. Приведем эти основные формулы.

Для коэффициента парной корреляции:

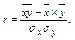
где r - коэффициент парной корреляции;

- среднее произведение признаков;

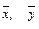- средние значения признаков;

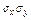- средние квадратические отклонения, определяемые для х по формуле 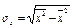и для y по формуле 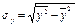, где первый член является средним значением квадратов, а второй - квадратом среднего значения признака.

Для корреляционного отношения при парной корреляции:

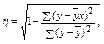
где 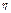- корреляционное отношение.

Для коэффициента множественной корреляции:

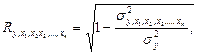
где 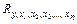- коэффициент множественной корреляции;

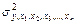- общая дисперсия зависимой переменной, характеризующая суммарное влияние на нее всех факторов;

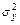- дисперсия зависимой переменной.

Эта формула имеет различные модификации. Так, в случае из­мерения влияния двух факторов на результат она принимает следую­щий вид:

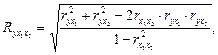
где r – коэффициенты парной корреляции.

В связи с тем, что точность (надежность) результатов изучения корреляционных связей в значительной мере зависит от количества сопоставляемых данных, которое часто бывает ограниченным, весьма полезно измерение погрешности (существенности) вычисленного коэффициента корреляции и корреляционного отношения.

Существенность r и ή проверяют по t-критерию, который полу­чается как отношение r или ή к их средней ошибке m_r. Для коэффициента корреляции это отношение можно записать так: .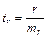

Если это отношение равно 3 или больше, коэффициент корреля­ции считается достоверным, то есть связь между признаками до­казана. Если же отношение коэффициента корреляции к средней ошибке меньше 3, связь между изучаемыми факторами нельзя счи­тать доказанной. Чтобы вывод был более надежным, рекомендуется брать величину отношения, равную не 3, а 4: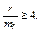

Средняя ошибка находится:

для коэффициента корреляции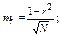

для корреляционного отношения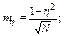

для коэффициента множественной корреляции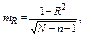

где N – число наблюдений;

n – количество факторов.