Способы представления производственных функций
При подготовке входной информации для экономико-математических задач могут быть успешно использованы производственные функции. В экономике сельского хозяйства это понятие объединяет все математически выраженные связи и зависимости результатов производства от затрат производственных факторов (урожайности культур – от доз внесения удобрений, удойности коров – от количества потребляемых кормов и т. п.).
Определение производственных функций позволяет разрабатывать параметры экономико-математических задач и наиболее целесообразно комбинировать различные производственные факторы для получения максимального количества сельскохозяйственной продукции при минимальных затратах труда и средств на ее производство. Кроме прогнозирования уровня результативного признака, производственные функции могут быть использованы для определения экономических оптимумов, коэффициентов эффективности и взаимозаменяемости факторов.
Производственные функции, как и функции математические, могут быть представлены различными способами. Они могут задаваться в виде таблиц, содержащих ряды значений аргумента и соответствующих значений функции. Табличный способ наиболее удобен в том случае, когда изучаются зависимости по данным непосредственных наблюдений. Производственные функции могут представляться графическим способом, одним из преимуществ которого является наглядность. По графику могут быть выявлены основные свойства исследуемой функции. Но этот способ имеет существенный недостаток. Точность определяемых значений зависимой переменной у при данных значениях факториального признака х ограничена. Наиболее распространенным является аналитический способ выражения производственных функций. В этом случае производственная функция представляет собой математическую модель многофакторного экономического процесса (или его отдельных сторон), которая в форме уравнения устанавливает связь между изучаемыми признаками. Это позволяет исчислить ожидаемое значение результата производства в зависимости от действующих на него факторов.
В отличие от экономико-математических моделей оптимального программирования, состоящих из ряда уравнений и неравенств, модель производственной функции в общем виде в большинстве случаев описывается одним уравнением, в котором результат производства представляется как функция п независимых величин-факторов:
у (производственный результат) = f (х1 х2, ..., хп),
где х1, х2, ..., хп - факторы производства.
Чтобы раскрыть неопределенность, скрывающуюся за этим математическим выражением, в процессе исследования находят конкретный вид алгебраического уравнения (уравнения регрессии), которое более или менее соответствовало бы исследуемым взаимосвязям.
Аналитический способ выражения производственных функций имеет существенные преимущества по сравнению с табличным и графическим. Он позволяет проанализировать влияние одного или нескольких факторов на производственный результат и определить с помощью приемов математического анализа различные коэффициенты, характеризующие изменения в процессе производства.
В связи с тем, что производственные функции представляют корреляционные связи, их обычно определяют путем обработки массовых данных методом корреляции.
Производственные функции раскрывают характер и степень влияния различных факторов на производственные результаты, поэтому для характеристики всего многообразия зависимостей в сельском хозяйстве нельзя использовать один вид уравнения. Имеется множество уравнений, с помощью которых могут быть выражены производственные функции в зависимости от существа исследуемого процесса и характера факторов, определяющих его результат (почва, климат, виды сельскохозяйственных культур и животных, характер производственных ресурсов и т. д.). Какой именно вид уравнения будет применен в каждом отдельном случае – зависит от качественного анализа и математической аппроксимации.
Однако некоторые виды уравнений благодаря их логическому смыслу, стройности математических расчетов выделяются из множества других и находят широкое применение в исследованиях. Эти виды уравнений принято называть производственными функциями даже в том случае, если они лишены конкретного экономического содержания.
Рассмотрим виды уравнений, которые чаще всего используются при определении производственных функций в сельском хозяйстве.
Самым простым видом уравнения является многочлен первой степени, графически изображаемый прямой линией. В общем виде его выражают следующим образом:
 или
или 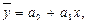
где  - зависимая переменная (результат производства);
- зависимая переменная (результат производства);
х - независимая переменная (фактор производства);
а и b - параметры уравнения.
Уравнение прямой обычно применяют в тех случаях, когда с возрастанием фактора х происходит пропорциональное увеличение или уменьшение результативного показателя. Это уравнение находит применение в исследованиях производственной функции, но чаще для ее описания используют уравнения криволинейных форм, которые в большей степени соответствуют истинному характеру связей и зависимостей в экономических процессах.
К производственным функциям, уравнения которых графически изображаются кривыми, относится, прежде всего, квадратическая функция параболического типа. Если есть основания ожидать, что величина результата производства у будет возрастать или убывать с увеличением фактора х и в границах его изменения возможен максимум или минимум величины у, то к уравнению прямой следует присоединить третий член b2х2, в результате чего получится многочлен второй степени или парабола второго порядка: 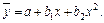
Так, определяя производственную функцию «урожайность - осадки», следует учитывать, что избыток влаги в почве может привести к снижению урожайности культур, поэтому необходимо введение в уравнение третьего члена b2х2.
В экономических расчетах в сельском хозяйстве часто используют параболу второго порядка, допускающую падающие и отрицательные приращения результата производства: 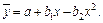
При исследовании производственных функций часто приходится рассматривать пары величин, обратно пропорциональных друг другу. Примером этого может быть зависимость между трудоемкостью и производительностью труда, нормой времени и нормой выработки, между себестоимостью и рентабельностью производства. Обратно пропорциональная зависимость в большинстве случаев предполагает уравнение гиперболы: 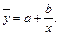
Эта зависимость основана на предположении, что часть расходов - а - растет пропорционально выпуску продукции, а остальная часть их - b - остается постоянной. Параметр а имеет конкретный экономический смысл потому, что уравнение построено на основе экономического анализа определенных производственных взаимосвязей.
Производственные функции могут быть выражены с помощью гиперболической формулы другого вида: 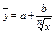 , где n>1.
, где n>1.
Эта функция основана на предположении, что издержки производства могут распределяться на возрастающие пропорционально выпуску продукции и возрастающие более медленно.
В практике аграрных экономических расчетов широко используются производственные функции степенного вида.
Степенная функция выражается следующим образом: 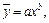 где b - коэффициент регрессии.
где b - коэффициент регрессии.
Эта функция удобна тем, что путем логарифмирования она приводится к линейной форме (относительно логарифмов х и у), которая решается проще, чем нелинейная. В то же время степенная функция, являясь криволинейной, обладает большей гибкостью и тем самым дает возможность лучше аппроксимировать сложные экономические взаимосвязи.
За рубежом к этому типу относится широко распространенная функция Кобба - Дугласа: 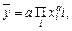
где хi - i-й аргумент;
аi - показатель степени i-го аргумента;
а - коэффициент пропорциональности;
П – знак произведения.
С помощью функции Кобба – Дугласа можно, например, определить численное значение дифференциальной ренты:

где i - факторы первой группы (качество почвы, осадки, температура, радиация, положение хозяйства), определяющие дифференциальную ренту I;
zk - факторы второй группы, интенсифицирующие сельское хозяйство (агротехника, сорта, качество семян, удобрения, породы животных, концентрация, механизация, организация труда, оплата труда и др.), определяющие дифференциальную ренту II;
а и β - показатели степени соответствующих аргументов хi и zk;
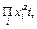 - величина, означающая степень влияния на доходность факторов первой группы.
- величина, означающая степень влияния на доходность факторов первой группы.
Если при определении производственной функции необходимо изучать влияние нескольких факторов на результат производства, то используют уравнение регрессии с несколькими независимыми переменными. Это уравнение выражает множественную или многофакторную корреляционную зависимость. Оно записывается так:
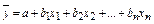 ,
,
где 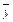 - результат производства;
- результат производства; 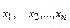 - факторы производства;
- факторы производства;
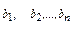 - коэффициенты регрессии, характеризующие влияние каждого фактора на исследуемый результат.
- коэффициенты регрессии, характеризующие влияние каждого фактора на исследуемый результат.
Графическим отображением этого уравнения является гиперплоскость в n+1 -мерном пространстве. Свободный член уравнения характеризует начальную ординату плоскости регрессии в этом пространстве. Его величина зависит от единиц измерения у и х. В отличие от свободного члена, который может не иметь самостоятельного значения и конкретного экономического смысла, остальные параметры (коэффициенты регрессии) всегда имеют определенный смысл. Они показывают, на сколько в среднем увеличилась бы независимая переменная у при изменении соответствующего фактора-аргумента х1 на одну единицу, если бы влияние других факторов, включенных в уравнение регрессии, было элиминировано. Однако при изменении на единицу данного фактора изменяются и корреляционно связанные с ним факторы, не включенные в уравнение регрессии. Поэтому каждый коэффициент регрессии bi показывает изменение у не только за счет соответствующего фактора хi , но и за счет тех связанных с ним факторов, которые не включены в уравнение регрессии. Решение многофакторных уравнений линейной регрессии производится с помощью метода наименьших квадратов.
В экономическом анализе применяют уравнения более сложного криволинейного типа, лучше описывающие многофакторные экономические взаимосвязи. Одним из таких уравнений является полином следующего вида:
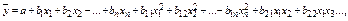
то есть разложение функции в ряд Тейлора.
Этот полином является довольно удобной аналитической формой для изучения экономических связей и зависимостей. Будучи криволинейным, он обладает достаточной гибкостью и в большинстве случаев уже при второй степени полинома хорошо описывает сложные зависимости. Однако применение его связано с трудностями вычисления аналитических показателей производственных функций. Кроме того, число степеней свободы уменьшается вследствие увеличения числа параметров.
В экономике широко применяется степенная функция вида:

Эта функция, как и степенная функция с одной переменной, приводится к линейному виду путем логарифмирования. Отметим еще, что при одинаковом числе факторов-аргументов степенная функция по сравнению с нелинейным полиномом имеет значительно меньшее число постоянных параметров, а, следовательно, и большее число степеней свободы при статистических оценках.
Дата добавления: 2015-08-14; просмотров: 1763;
