Экономические характеристики производственных функций

Производственные функции служат весьма эффективным средст­вом углубленного изучения экономических процессов. Умелое их применение может сыграть важную роль в принятии оптимальных решений. На основе производственных функций можно получить ряд дополнительных характеристик, которые не могут дать тради­ционные методы корреляции. Их получают путем дифференцирова­ния, то есть вычисления производных. В экономике в основном при­меняют недробные функции, которые за исключением отдельных случаев являются непрерывными, поэтому производные от них мож­но находить с небольшой погрешностью применительно к экономиче­ским параметрам производства.

Одним из основных аналитических показателей, получаемых на основе производственных функций, является дополнительный продукт фактора¹. Дополнительный продукт фактора – это прирост продук­ции у за счет увеличения данного фактора на единицу при неизмен­ной величине других факторов. Аналитическим выражением допол­нительного продукта фактора является первая частная производная производственной функции по этому фактору-аргументу: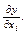

Геометрически дополнительный продукт фактора х характеризует изменение у в связи с изменением х и называется кривой затрат - выпуска (рис. 53). Размер дополнительного продукта выражают танген­сы углов наклона этой кривой.

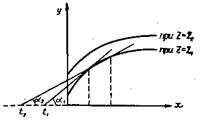
Рис. 53 - Кривые затрат – выпуска

Уравнения дополнительных продуктов могут быть использова­ны для нахождения таких значений факторов, при которых обеспе­чивается максимальный выход продукции. Приравняв уравнение дополнительных продуктов всех факторов нулю и решая получен­ную систему уравнений, можно определить значения факторов, максимизирующих выход продукции.

Важным аналитическим показателем, применяемым при исследовании производственных функций, является производственный коэффициент эластичности. Этот коэффициент представляет собой соотношение темпов прироста продукции у и того или иного фактора x_i, то есть выражает степень реакции у на относительное изменение x_i. Приближенно коэффициент эластичности показывает, на сколько процентов изменяется в среднем выход продукции при изменении данного фактора на 1% (при неизменной величине других факторов).

Коэффициент эластичности может быть исчислен либо путем де­ления относительного прироста продукции на относительный при­рост фактора:

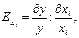
либо как отношение дополнительного продукта к среднему выходу продукции на единицу фактора (к отдаче фактора):

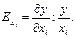
Производственные функции дают возможность находить раз­личные комбинации значений факторов, при которых обеспечи­вается данный (фиксированный) выход продукции у. Для этого сле­дует решить уравнение производственной функции относительно одного из факторов, условно считая его «зависимой величиной». Придавая затем какие-либо фиксированные значения, получим ряд уравнений, показывающих, какова должна быть величина данного фактора, чтобы при тех или иных значениях других факторов обе­спечивалось заданное значение у.

Производственные функции допу­скают различное сочетание значений фактора, обеспечивающих одинаковый выход продукции. Если одинаковое увеличение у может быть получено при различных комбинациях факторов, то можно считать эти факторы взаимозаменяемыми даже в том случае, если технологически они и не могут заме­нить друг друга.

В связи с возможностью заменяемости факторов возникает вопрос о ее нормах. Норма, по которой один фактор заменяет другой при сохра­нении выхода продукции на заданном уровне, называется дифференциаль­ной (предельной) нормой заменяемости. Уравнение предельной нор­мы заменяемости может быть полу­чено:

как производная одного фактора по другому, то есть как производная уравнения изоквант: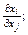

как обратное отношение дополнительных продуктов-факторов, взятое со знаком минус: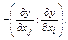

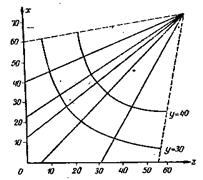
Рис. 54 - Изокванты и изоклинали функции у=5+0,6х+0,7z-0.005x²-0.006z²+0.002xz

Предельная норма заменяемости 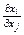показывает, насколько нужно увеличить фактор x_i, чтобы небольшое уменьшение факторов x_i не изменило величину выхода продукции.

Геометрически предельная норма заменяемости 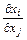представляет тангенс угла наклона изокванты в данной точки, т.е. тангенс угла между касательной к изокванте в той или иной точке и осью ОХ.

Используя уравнение предельной нормы заменяемости, можно определить так называемое пути расширения, т.е. пути увеличения выхода продукции – изоклинали. Они показывают, в каком направлении должна изменяться комбинация (сочетание) факторов, чтобы увеличивался выход продукции, если предельная норма заменяемости остается постоянной.

Уравнение изоклиналей может быть получено из уравнения предельной нормы заменяемости путем приравнивания его к определенной, желательной нам величине и решения относительно одного из факторов.

Предельная норма заменяемости 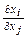показывает, насколько нужно увеличить фактор х_i,чтобы при уменьшении фактора х_j на небольшую величину выход продукции остался неизменным.

Придавая предельной норме заменяемости нужные значения, получим ряд изоклиналей. В нашем примере изоклинали графически изображаются прямыми линиями, одна из которых (при k= 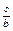) проходит через начало координат. Изоклинали пересекаются в точ­ке, соответствующей максимальному выходу продукции (вершина «холма») и соединяют точки на изоквантах с равными предельными нормами замещения факторов, то есть точки с равными углами нак­лона на расположенных в возрастающем порядке изоквантах. Две изоклинали являются как бы линиями «водораздела», ограничивающими нулевые и бесконечные нормы замещения факторов. Эти изоклинали называются разграничительными линиями. Они изображены пунктиром на рисунке 54.