Использование зондирующего сигнала

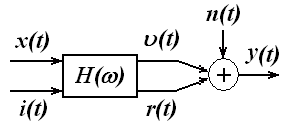
В некоторых инженерных приложениях входной процесс 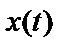не наблюдается, но имеется возможность подать на вход системы известный зондирующий сигнал 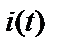, независимый от естественного входа (рисунок 2.7).

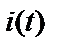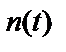Разумно предположить, что не зависит от и , а 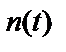не зависит от 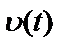и .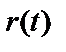

Применение финитного преобразования Фурье к реализациям достаточно большой длины 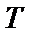приводит к следующим соотношениям между величинами, указанными на рисунке 2.7:

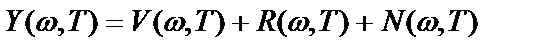, (2.57)

где ,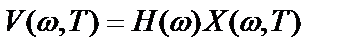

.

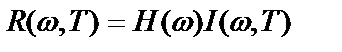– естественный ненаблюдаемый входной процесс;

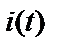– известный наблюдаемый зондирующий сигнал;

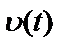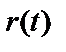, – ненаблюдаемые реакции на и 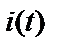соответственно;

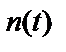– ненаблюдаемый шум на выходе системы;

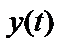– суммарный наблюдаемый процесс на выходе

Рисунок 2.7 – Система с зондирующим сигналом и шумом на выходе

По предположению следующие взаимные спектральные плотности равны нулю:

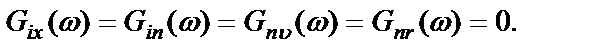
Поэтому с учетом (2.57) для регистрируемых спектральных плотностей имеем

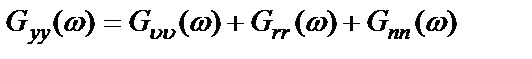, (2.58)

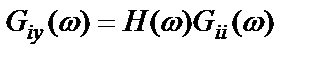. (2.59)

Поскольку процесс не наблюдаем, для оценки частотной характеристики системы невозможно использовать стандартную формулу через взаимную спектральную плотность

.

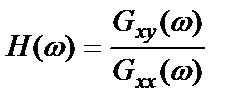Однако соотношение (2.59) показывает, что при известном зондирующем сигнале имеет место равенство

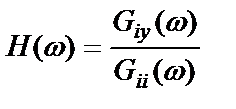, (2.60)

которое дает несмещенную оценку 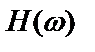независимо от шума на выходе и каких-либо предположений относительно естественного входа .

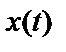В качестве зондирующего сигнала 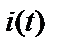часто выбирают ограниченный по частоте белый шум, имеющий постоянную спектральную плотность в широкой полосе частот .

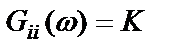В этом случае частотная характеристика равна

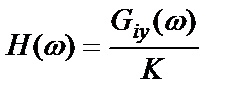. (2.61)

Как только частотная характеристика системы определена по формулам (2.60) или (2.61) , зондирующий сигнал отключают и уравнение (2.57) принимает вид

,

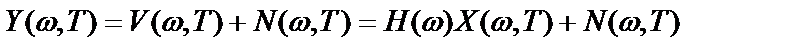откуда, наблюдая только процесс 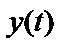, получают выходную спектральную плотность

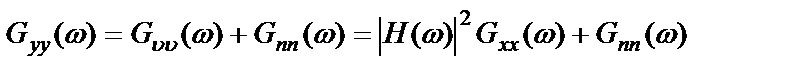. (2.62)

Если вклад шума на выходе системы невелик 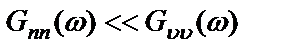, то справедливо приближенное равенство

,

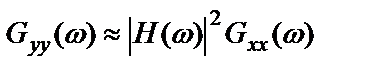следовательно

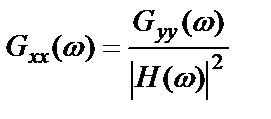. (2.63)

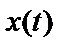Формула (2.63) дает полезную информацию о спектральной плотности , даже если процесс не наблюдается. В частности, 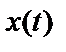может быть собственным шумом системы на входе, а 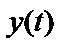– собственным шумом на выходе, вызванном .

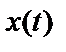Контрольные вопросы

1. Перечислите свойства идеальной системы и объясните их смысл.

2. Сформулируйте определение импульсной характеристики системы.

3. Каким преобразованием связаны между собой частотная и импульсная характеристики идеальной системы?

4. Перечислите способы расчета амплитудной частотной характеристики системы.

5. Сформулируйте теорему о спектре производной.

6. Запишите основные спектральные соотношения для идеальной системы.

7. Осуществите расчет функции когерентности для идеальной системы.

8. Как влияет наличие некоррелированных шумов на входе и выходе системы на спектральные соотношения?

9. Запишите выражение для частотной характеристики системы с обратной связью.

10. С какой целью может использоваться зондирующий сигнал?

Литература

1. Сергиенко, А.Б. Цифровая обработка сигналов / А.Б. Сергиенко. – М: Питер, 2002.– 604 с.

2. Садовский, Г.А. Теоретические основы информационно-измерительной техники / Г.А. Садовский. – М.: Высшая школа, 2008. – 480 с.

3. Бендат, Д. Применение корреляционного и спектрального анализа / Д. Бендат, А. Пирсол. – М.: Мир, 1983. – 312 с.

4. Бендат, Д. Измерение и анализ случайных процессов / Д. Бендат, А. Пирсол. – М.: Мир, 1974. – 464 с.