Влияние внешнего шума

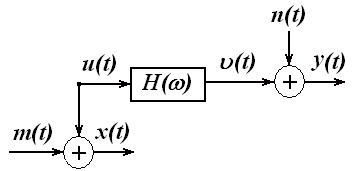
Рассмотрим теперь более реалистичную модель системы, учитывающую влияние некоррелированного внешнего шума на наблюдения входного и выходного процессов (рисунок 2.5).

Предполагаем, что шумы не коррелированны между собой и с сигналами, т.е. для взаимных спектральных плотностей справедливо следующее соотношение:

.

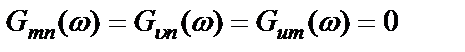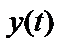, – наблюдаемые процессы на входе и выходе;

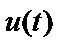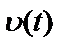, – ненаблюдаемые истинные процессы на входе и выходе;

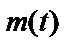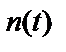, – ненаблюдаемые шумы на входе и выходе

Рисунок 2.5 – Система с внешним шумом на входе и выходе

Наблюдаемые реализации входных и выходных процессов имеют вид

,

,

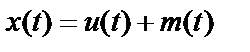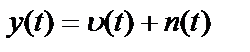где 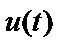, 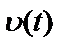– истинные сигналы;

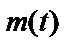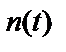, – шумы на входе и выходе соответственно.

Из основных спектральных соотношений (2.25) для идеальной системы получим

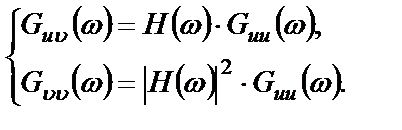(2.42)

Однако в действительности наблюдаются спектральные плотности 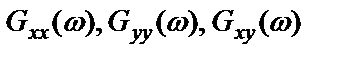, где, согласно п.2.5, 2.6,

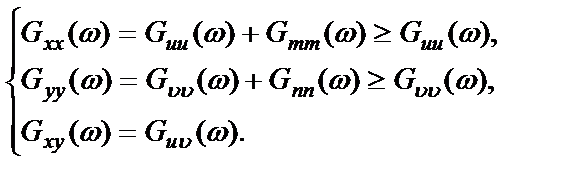(2.43)

Истинная функция когерентности равна

,

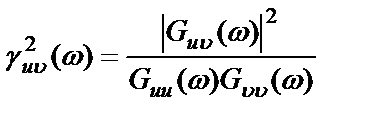а наблюдаемая функция когерентности имеет вид

.

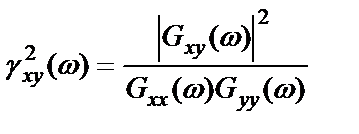Из формул (2.42), (2.43) находим

,

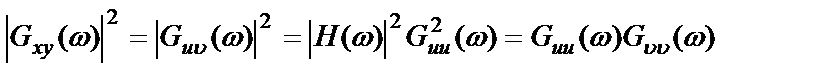откуда

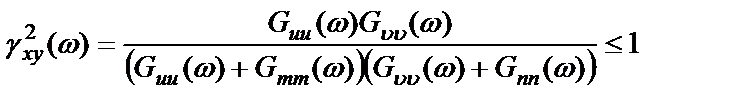. (2.44)

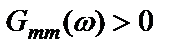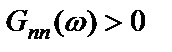Неравенство (2.44) будет строгим, если или , что на практике всегда имеет место.

Для рассматриваемой системы можно получить оценку частотной характеристики по наблюдениям процессов , , 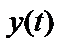используя соотношения

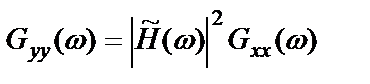, (2.45)

, (2.46)

где 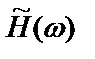– наблюдаемая частотная характеристика.

Выражение (2.45) позволяет оценить квадрат амплитудной характеристики по спектрам

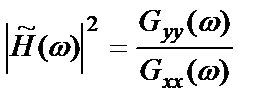, (2.47)

а выражение (2.46) – частотную характеристику по взаимному спектру

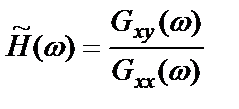. (2.48)

Подстановка выражений (2.43) в (2.47) дает

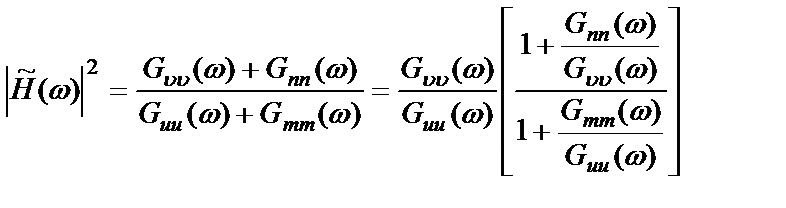
или

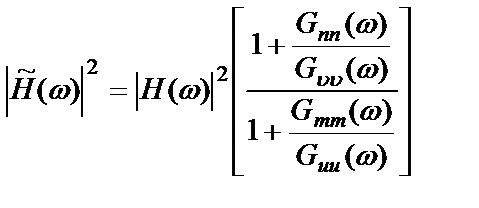, (2.49)

где 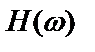– истинная частотная характеристика согласно (2.42).

Очевидно, что всегда дает смещенную оценку 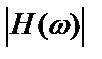, ес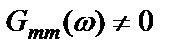ли или .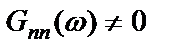

Подставляя выражения (2.43) в (2.48) и учитывая (2.42), получим

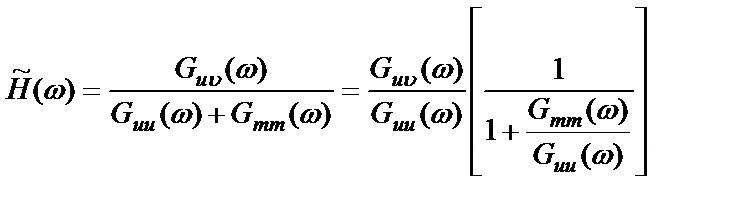
или

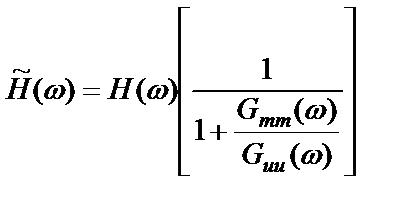, (2.50)

откуда видно, что если 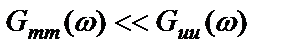, то 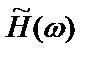даст несмещенную оценку частотной характеристики 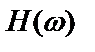независимо от значения спектральной плотности шума на выходе .

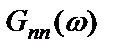Соотношения (2.49), (2.50) позволяют заключить, что взаимно-спектральные методы оценки частотной характеристики имеют преимущество над спектральными в том случае, когда на выходе системы имеется внешний шум. Кроме того, взаимно-спектральные методы позволяют не утратить информацию о фазовой составляющей частотной характеристики системы.