Система с внешним шумом на входе
Рассмотрим второй случай, когда некоррелированный внешний шум присутствует только в измерениях входного процесса  , не проходя при этом через систему (рисунок 2.4).
, не проходя при этом через систему (рисунок 2.4).

 – наблюдаемый входной процесс;
– наблюдаемый входной процесс; 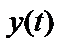 – наблюдаемый выходной процесс;
– наблюдаемый выходной процесс; 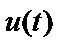 – ненаблюдаемый истинный входной процесс;
– ненаблюдаемый истинный входной процесс;
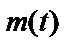 – ненаблюдаемый входной шум
– ненаблюдаемый входной шум
Рисунок 2.4 – Система с внешним шумом на входе
Предполагаем также, что все процессы в системе относятся к стационарным, а их средние значения равны нулю
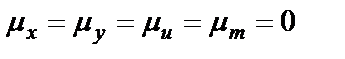 .
.
Наблюдаемая реализация входного процесса принимает вид
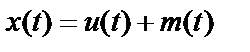 , (2.37)
, (2.37)
где 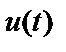 – ненаблюдаемый истинный входной процесс;
– ненаблюдаемый истинный входной процесс;
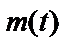 – ненаблюдаемый некоррелированный входной шум.
– ненаблюдаемый некоррелированный входной шум.
Наблюдаемый входной спектр мощности с учетом некоррелированности 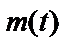 и
и 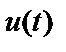 и выражения (2.37) состоит из суммы
и выражения (2.37) состоит из суммы
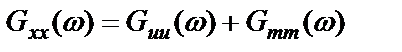 . (2.38)
. (2.38)
Поскольку внешний шум через систему не проходит, то справедливо равенство
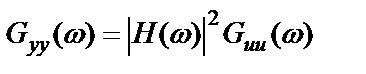 . (2.39)
. (2.39)
Для вывода выражения для взаимного спектра мощности наблюдаемых процессов на входе и выходе системы рассмотрим произведение мгновенных значений процессов в два различных момента времени
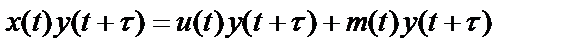 ,
,
откуда
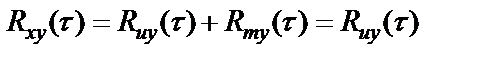 ,
,
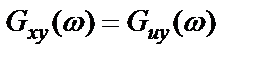 , (2.40)
, (2.40)
где 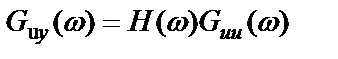 – взаимная спектральная плотность истинных процессов на входе и выходе системы.
– взаимная спектральная плотность истинных процессов на входе и выходе системы.
Рассмотрим произведение функции когерентности между процессами 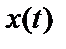 и
и 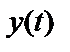 и наблюдаемым входным спектром:
и наблюдаемым входным спектром:
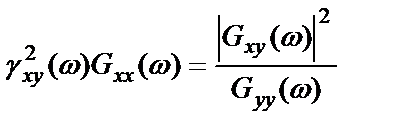 .
.
Учитывая равенства (2.38), (2.39), получим:
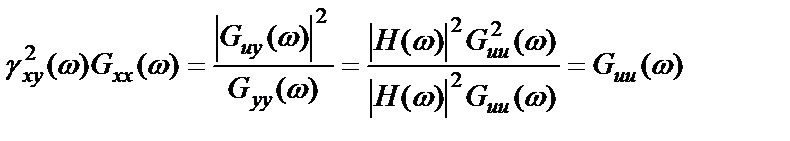 ,
,
что соответствует спектру ненаблюдаемого истинного входного процесса 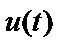 .
.
Произведение в правой части равенства
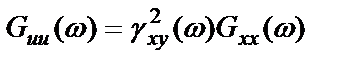 , (2.41)
, (2.41)
носит название когерентного спектра входного процесса.
Отношение шума к истинному сигналу на входе рассматриваемой системы принимает вид, совпадающий с аналогичной величиной для системы с шумом на выходе:
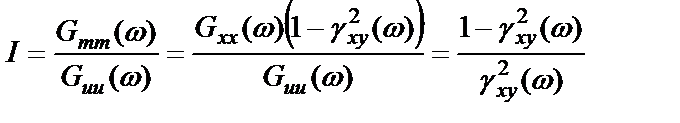 .
.
К основным спектральным соотношениям для системы с некоррелированным внешним шумом на входе относятся выражения (2.39)-(2.41).
Дата добавления: 2015-08-14; просмотров: 627;
