Система с внешним шумом на выходе
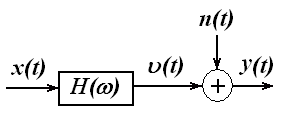
Рассмотрим систему, в которой некоррелированный внешний шум присутствует только на ее выходе (рисунок 2.3). Предполагаем, что все процессы в системе относятся к стационарным, а их средние значения равны нулю
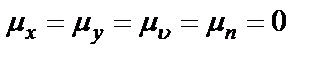 .
.
Наблюдаемая реализация выходного процесса примет вид
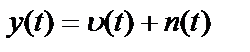 , (2.28)
, (2.28)
где 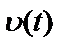 – ненаблюдаемый истинный выходной процесс;
– ненаблюдаемый истинный выходной процесс;
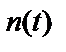 – ненаблюдаемый некоррелированный выходной шум.
– ненаблюдаемый некоррелированный выходной шум.
 – наблюдаемый входной процесс;
– наблюдаемый входной процесс; 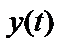 – наблюдаемый выходной процесс;
– наблюдаемый выходной процесс; 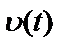 – ненаблюдаемый истинный выходной процесс;
– ненаблюдаемый истинный выходной процесс;
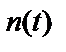 – ненаблюдаемый выходной шум
– ненаблюдаемый выходной шум
Рисунок 2.3 – Система с внешним шумом на выходе
Произведение мгновенных значений наблюдаемого выходного процесса в два различных момента времени равно
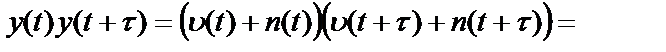
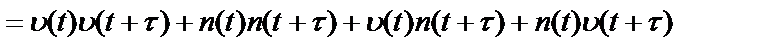 ,
,
откуда после усреднения получим следующее соотношение для ковариационных функций:
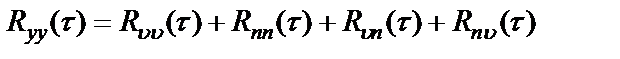 . (2.29)
. (2.29)
В силу не коррелированности шума имеем
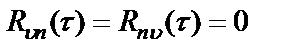 . (2.30)
. (2.30)
В результате преобразования Фурье над выражением (2.29) с учетом (2.30) наблюдаемый выходной спектр мощности системы примет вид суммы идеального линейного выхода 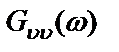 , порожденного преобразованием
, порожденного преобразованием  посредством
посредством 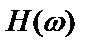 , и шума на выходе
, и шума на выходе 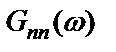 , т.е.
, т.е.
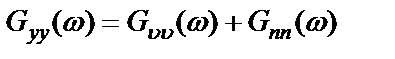 , (2.31)
, (2.31)
где 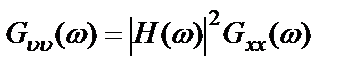 – спектр мощности истинного (полезного) выходного процесса.
– спектр мощности истинного (полезного) выходного процесса.
Для взаимной спектральной плотности наблюдаемых процессов на входе и выходе аналогично получим:
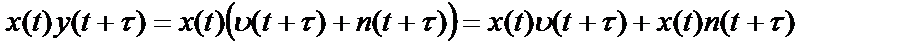 ,
,
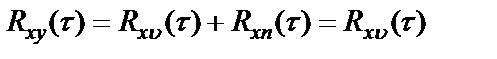 ,
,
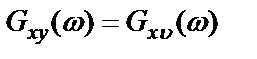 , (2.32)
, (2.32)
где 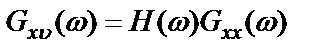 – взаимная спектральная плотность истинных процессов на входе и выходе системы.
– взаимная спектральная плотность истинных процессов на входе и выходе системы.
Таким образом, согласно выражениям (2.31), (2.32), наблюдаемый выходной спектр мощности 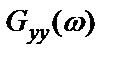 дает смещенную оценку истинного выходного спектра
дает смещенную оценку истинного выходного спектра 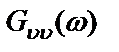 , а наблюдаемый взаимный спектр
, а наблюдаемый взаимный спектр 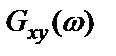 – несмещенную оценку
– несмещенную оценку 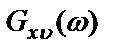 .
.
Учитывая это, можно рассчитать спектральную плотность ненаблюдаемого истинного выходного процесса 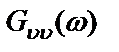 через регистрируемые процессы:
через регистрируемые процессы:
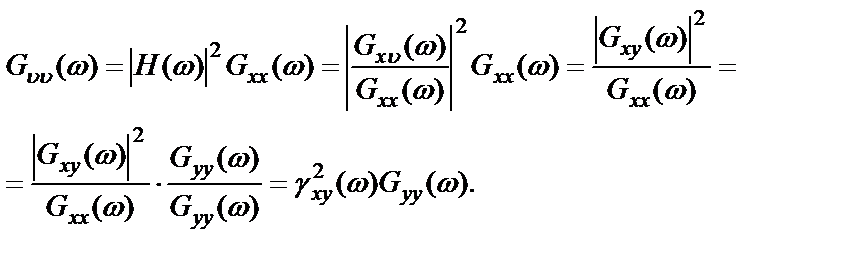
Произведение в правой части равенства
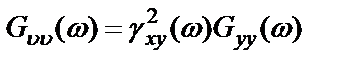 (2.33)
(2.33)
носит название когерентного спектра выходного процесса.
Соотношения (2.31)-(2.33) являются основными спектральными соотношениями для системы с внешним некоррелированным шумом на выходе.
Согласно выражению (2.33), функцию когерентности можно истолковать как долю спектра истинного выходного процесса 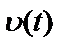 в наблюдаемом выходном спектре:
в наблюдаемом выходном спектре:
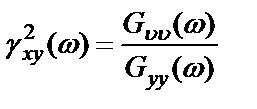 . (2.34)
. (2.34)
Выходной спектр шума тогда равен
 (2.35)
(2.35)
и может быть интерпретирован как часть выходного спектра, не связанная с линейным преобразованием процесса  на частоте
на частоте 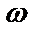 .
.
Соотношения (2.34), (2.35) позволяют найти отношение шума к истинному сигналу на выходе системы:
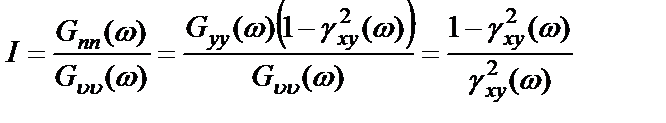 , (2.36)
, (2.36)
откуда следует, что 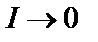 при
при 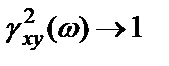 и
и  при
при 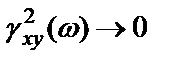 .
.
Дата добавления: 2015-08-14; просмотров: 638;
