Частотные характеристики

Динамические свойства физической системы принято описывать не только ее импульсной характеристикой, но и некоторым линейным преобразованием над ней. Причем вид этого преобразования зависит от конкретной задачи. В случае идеальной системы пользуются преобразованием Фурье, позволяющим непосредственно описать динамические характеристики системы в частотной области.

Прямое преобразование Фурье над импульсной характеристикой определяет частотную характеристику системы

,

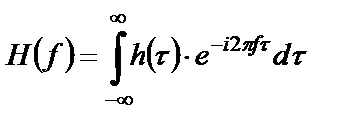или

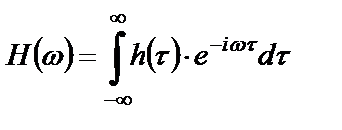. (2.7)

Импульсная характеристика связана с частотной через обратное преобразование Фурье

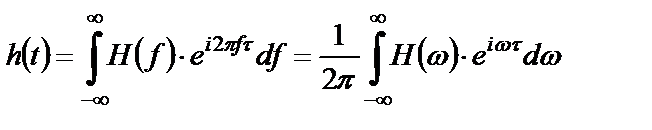. (2.8)

Для физически осуществимой системы выражение (2.7) принимает вид

. (2.9)

В частотной характеристике выделяют действительную и мнимую составляющие:

,

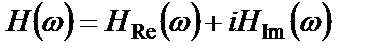где – действительная часть функции ;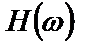

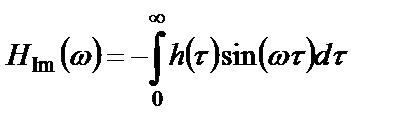– мнимая часть функции .

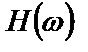Поскольку частотная характеристика является комплексной величиной, то ее можно представить в показательном виде

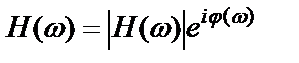, (2.10)

где 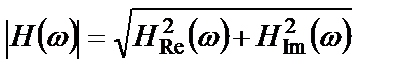– амплитудная частотная характеристика системы (АЧХ);

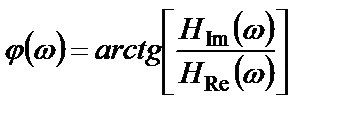– фазовая частотная характеристика (ФЧХ).

На практике АЧХ и ФЧХ можно получить простым способом, если представить частотную характеристику в виде отношения

,

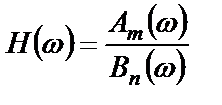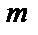где – многочлены степеней и 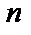соответственно.

Тогда расчет амплитудной и фазовой составляющих функции 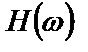проводят по следующим соотношениям:

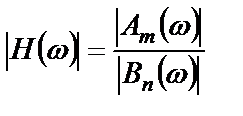, (2.11)

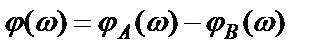. (2.12)

Амплитудная и фазовая составляющие частотной характеристики системы имеют очевидную физическую интерпретацию. Если на вход системы поступает гармонический сигнал

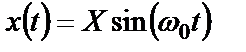
с амплитудой 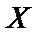и частотой 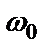, то на выходе будет наблюдаться также гармонический сигнал с той же частотой 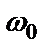, но, в общем случае, с измененной амплитудой 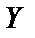и смещенный по фазе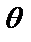

.

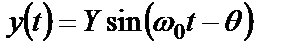Изменения параметров выходного сигнала связаны с особенностями частотной характеристики звена.

Амплитудная частотная характеристика системы на частоте входного сигнала представляет собой отношение амплитуды установившегося выходного гармонического сигнала к амплитуде входного гармонического сигнала

,

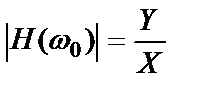где 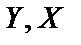– амплитуды выходного и входного сигналов соответственно.

Фазовая частотная характеристикасистемы на частоте входного сигнала показывает, на сколько выходной сигнал сдвинут по фазе (углу) относительно входного сигнала

.

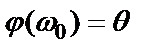Помимо выражения (2.7), частотная характеристика системы может быть также получена и через отношение спектров выходного 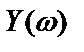и входного 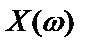сигналов:

. (2.13)

Под спектрами сигналов понимают результат прямого преобразования Фурье над самими сигналами:

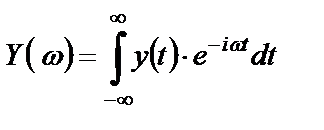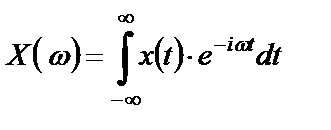, , (2.14)

где 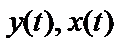– сигналы во временной области.

Частотная характеристика идеальной системы, а также ее амплитудная и фазовая составляющие обладают следующими свойствами симметрии:

,

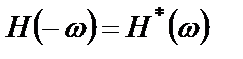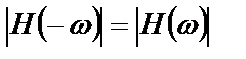, (2.15)

.

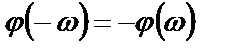Если за системой с частной характеристикой 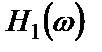расположена вторая система с частотной характеристикой 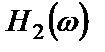и между системами не включено нагрузки и отсутствует обратная связь, то эту сложную систему можно в целом охарактеризовать частотной характеристикой 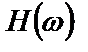, такой, что

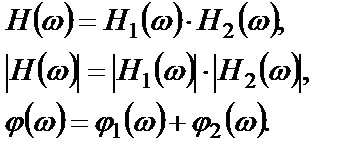(2.16)

Таким образом, для каскада из двух систем при отсутствии между ними нагрузки или обратной связи амплитудные частотные характеристики перемножаются, а фазовые частотные характеристики складываются.

Частотная характеристика линейной системы с постоянными параметрами является только функцией частоты и не зависит ни от времени, ни от интенсивности входного процесса. Если же система не линейна, то ее частотная характеристика будет зависеть также и от интенсивности входного процесса. Характеристика системы с переменными параметрами является также функцией времени.

При прохождении через линейные системы спектры сигналов подвергаются преобразованиям в соответствии с комплексной частотной характеристикой системы: изменяются как амплитудный спектр сигнала, так и фазы спектральных составляющих.

При подобных преобразованиях необходимо учитывать основные теоремы о спектрах.