Спектральная плотность мощности

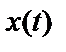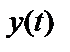Взаимная спектральная плотность мощности(взаимный спектр мощности) двух реализаций и стационарных эргодических случайных процессов 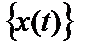и определяется как прямое преобразование Фурье над их взаимной ковариационной функцией

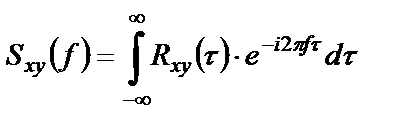(1.32)

или, с учетом соотношения между круговой и циклической частотами ,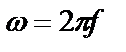

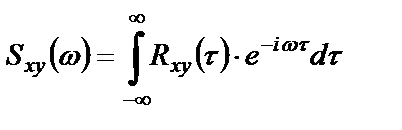. (1.33)

Обратное преобразование Фурье связывает взаимные ковариационную функцию и спектральную плотность мощности:

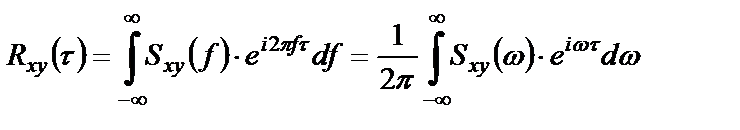. (1.34)

Аналогично (1.32), (1.33) вводится спектральная плотность мощности(спектр мощности) случайного процесса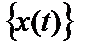

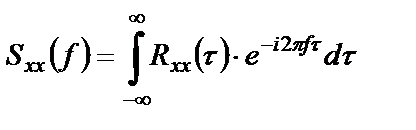(1.35)

или

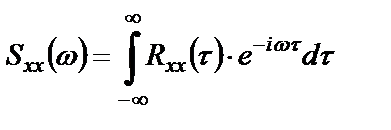. (1.36)

Функция обладает свойством четности:

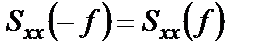. (1.37)

Для взаимной спектральной плотности справедливо следующее соотношение:

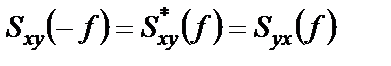, (1.38)

где 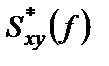– функция, комплексно сопряженная к .

Введенные выше формулы для спектральных плотностей определены как для положительных, так и для отрицательных частот и носят название двухсторонних спектральных плотностей. Они удобны при аналитическом изучении систем и сигналов. На практике же пользуются спектральными плотностями, определенными только для неотрицательных частот и называемыми односторонними (рисунок 1.14):

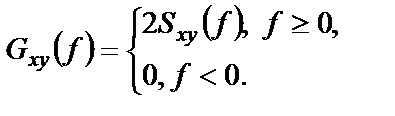(1.39)

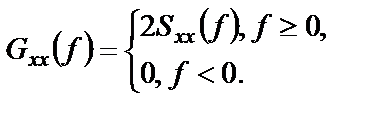(1.40)

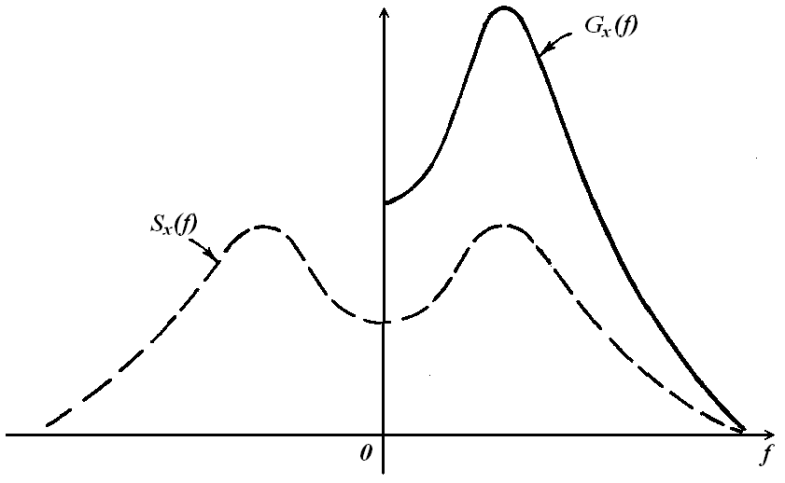
Рисунок 1.14 – Односторонняя и двусторонняя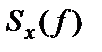

спектральные плотности

Выведем выражение, связывающее одностороннюю спектральную плотность стационарного СП с его ковариационной функцией:

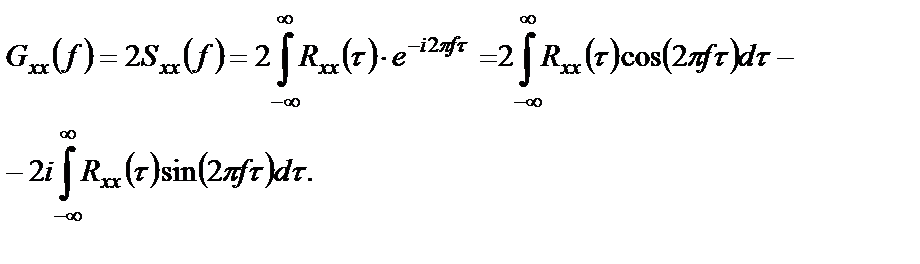
Учтем свойство четности для ковариационной функции стационарного СП и функции косинус, свойство нечетности для функции синус, а также симметричность пределов интегрирования. В результате второй интеграл в полученном выше выражении обращается в нуль, а в первом интеграле можно сократить вдвое пределы интегрирования, удвоив при этом коэффициент:

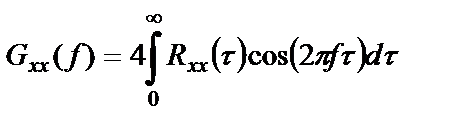. (1.41)

Очевидно, что спектральная плотность мощности случайного процесса 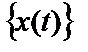является действительной функцией.

Аналогично можно получить обратное соотношение:

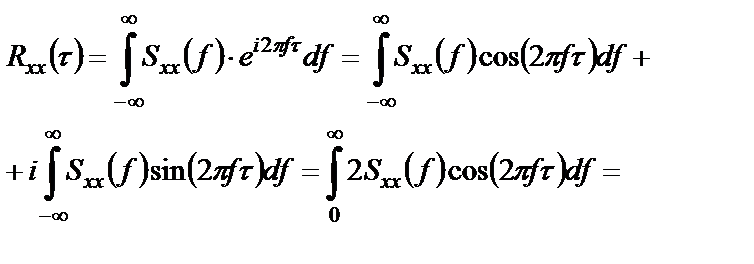
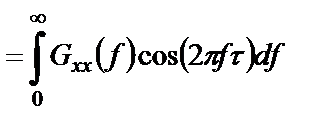. (1.42)

Из выражения (1.42) при 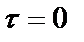следует, что

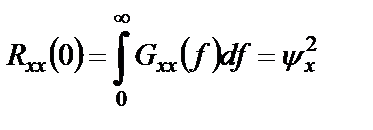. (1.43)

Это означает, что общая площадь под графиком односторонней спектральной плотности равна среднему квадрату случайного процесса. Другими словами, односторонняя спектральная плотность интерпретируется как распределение среднего квадрата процесса по частотам.

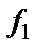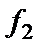Площадь под графиком односторонней плотности, заключенная между двумя произвольными значениями частоты и , равна среднему квадрату процесса в этой полосе частот спектра (рисунок 1.15):

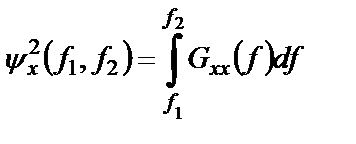. (1.44)

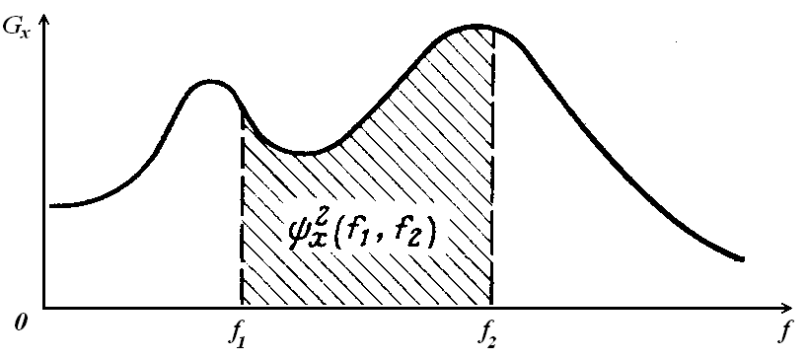
Рисунок 1.15 – Свойство спектральной плотности

Взаимная спектральная плотность мощности является комплексной величиной, поэтому ее можно представить в показательной форме записи через модуль и фазовый угол:

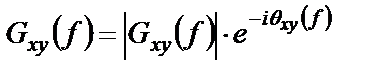, (1.45)

где 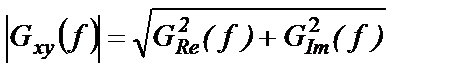– модуль;

– фазовый угол;

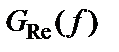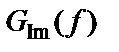, – действительная и мнимая части функции соответственно.

Модуль взаимной спектральной плотности входит в важное неравенство

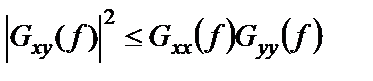. (1.46)

Это неравенство позволяет определить функцию когерентности (квадрат когерентности), которая аналогична квадрату нормированной корреляционной функции:

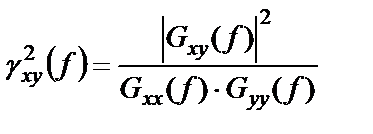, (1.47)

причем .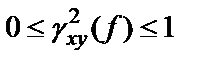

Второй способ введения спектральных плотностей состоит в непосредственном преобразовании Фурье случайных процессов.

Пусть 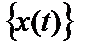и – два стационарных эргодических случайных процесса, для которых финитные преобразования Фурье 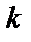-х реализаций длины 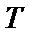определяют в виде

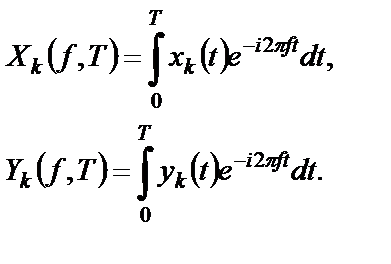(1.48)

Двусторонняя взаимная спектральная плотность этих случайных процессов вводится с использованием произведения 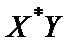через соотношение

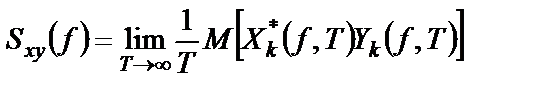, (1.49)

где оператор математического ожидания 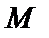означает операцию усреднения по индексу .

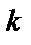Расчет двусторонней спектральной плотности случайного процесса 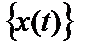осуществляют по соотношению

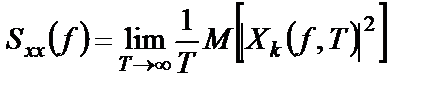. (1.50)

Аналогично вводятся и односторонние спектральные плотности:

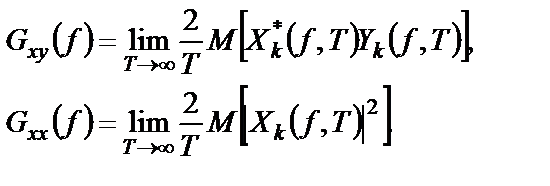(1.51)

Функции 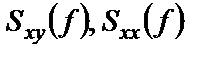, определенные формулами (1.49), (1.50), идентичны соответствующим функциям, определенным соотношениями (1.32), (1.33) как преобразования Фурье над ковариационными функциями. Это утверждение носит называние теоремы Винера-Хинчина.