Плотность распределения вероятности

Плотность распределения вероятности случайного процесса определяет среднюю вероятность того, что значения процесса в произвольный момент времени будут заключены в определенном интервале.

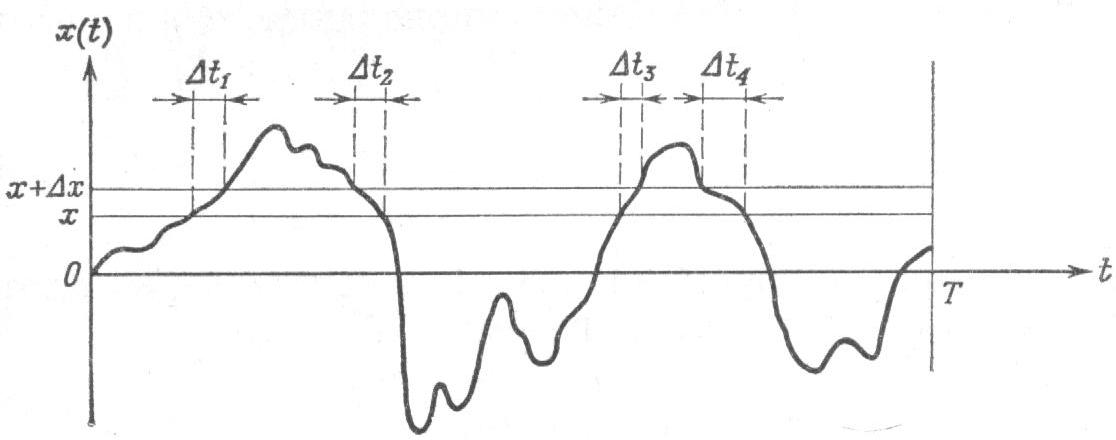
Рассмотрим некоторую реализацию СП как функцию времени (рисунок 1.9).

– реализация СП, – время наблюдения

Рисунок 1.9 – Определение плотности распределения вероятности

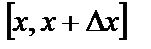Вероятность того, что значения попадут в интервал можно найти, вычисляя отношени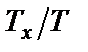е , где 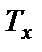– суммарная продолжительность нахождения значений процесса в интервале 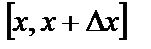за время наблюдения . При стремлении к бесконечности это отношение все точнее будет описывать вероятность такого события:

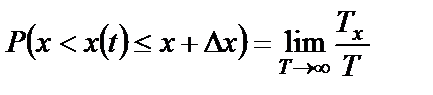, (1.20)

где .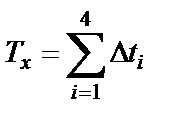

При малых 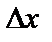плотность распределения вероятности СП определяется соотношением

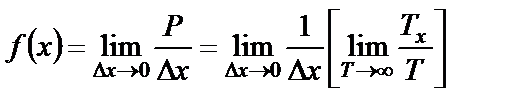. (1.21)

Зная плотность распределения вероятности СП, можно рассчитать его усредненные характеристики, используя, например, следующие соотношения для среднего значения и среднего квадрата:

, .

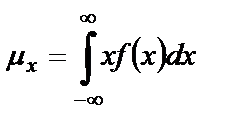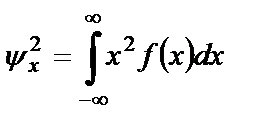Во многих практических задачах приходится вычислять математическое ожидание некоторой функции 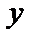от случайной величины 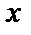, имеющей плотность распределения вероятности 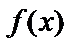. Такое вычисление выполняется по следующей формуле:

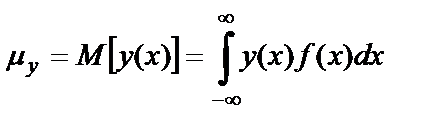. (1.22)

При анализе случайных явлений используется большое число различных плотностей вероятности. Рассмотрим две из них, которые хорошо описывают широкий класс практически важных случайных явлений.

Плотности большого числа случайных процессов хорошо аппроксимируются выражением вида

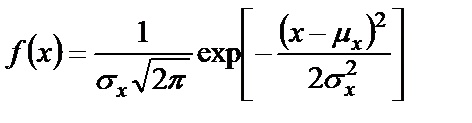, (1.23)

где 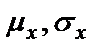– среднее значение и среднеквадратичное отклонение соответственно.

Функцию (1.23) называют нормальной, или гауссовской, плотностью, она характеризует случайный шум (широкополосный или узкополосный), для которого среднее значение наиболее вероятно. График нормальной плотности имеет колоколообразную форму (рисунок 1.10).

Рисунок 1.10 – Нормальная плотность распределения

Важность нормального распределения определяется широким применением на практике центральной предельной теоремы, которая формулируется следующим образом: сумма большого числа совместно действующих независимых случайных величин распределена в общем случае по закону, близкому к нормальному.

По двум причинам желательно иметь возможность предполагать, что случайный процесс имеет нормальную плотность распределения:

1) нормальное распределение полностью определяется только двумя параметрами – средним значением и среднеквадратичным отклонением;

2) все линейные операции такие, как интегрирование, дифференцирование, преобразование Фурье, выполняемые над нормально распределенными случайными величины, дают в результате также нормально распределенные величины.

Наиболее распространенный вид детерминированных процессов – это периодические процессы, разлагаемые на гармонические составляющие. Для описания одной такой составляющей не требуется вероятностных понятий, поскольку ее точное значение в любой момент времени вычисляется по формуле

.

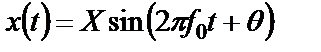Однако гармоническое колебание можно рассматривать также как выборочную функцию случайного процесса 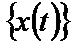, где начальная фаза каждой выборочной функции 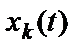является случайной величиной, равномерно распределенной в интервале .

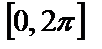Плотность распределения вероятности такого случайного гармонического процесса определяется формулой

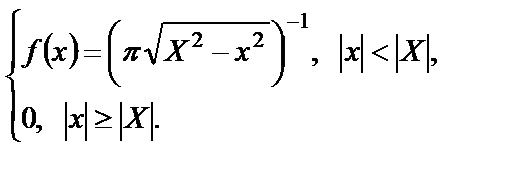(1.24)

График функции (1.24) имеет чашеобразную форму (рисунок 1.11), откуда видно, что плотность гармонического процесса достигает минимума в точке с координатой, равной среднему значению .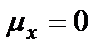

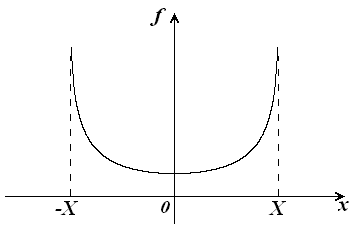
Рисунок 1.11 – Плотность распределения гармонического процесса