Стационарные случайные процессы. Случайный процесс в любой момент времени может быть описан путем усреднения величин по множеству выборочных функций
Случайный процесс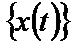 
в любой момент времени может быть описан путем усреднения величин по множеству выборочных функций, образующих случайный процесс.
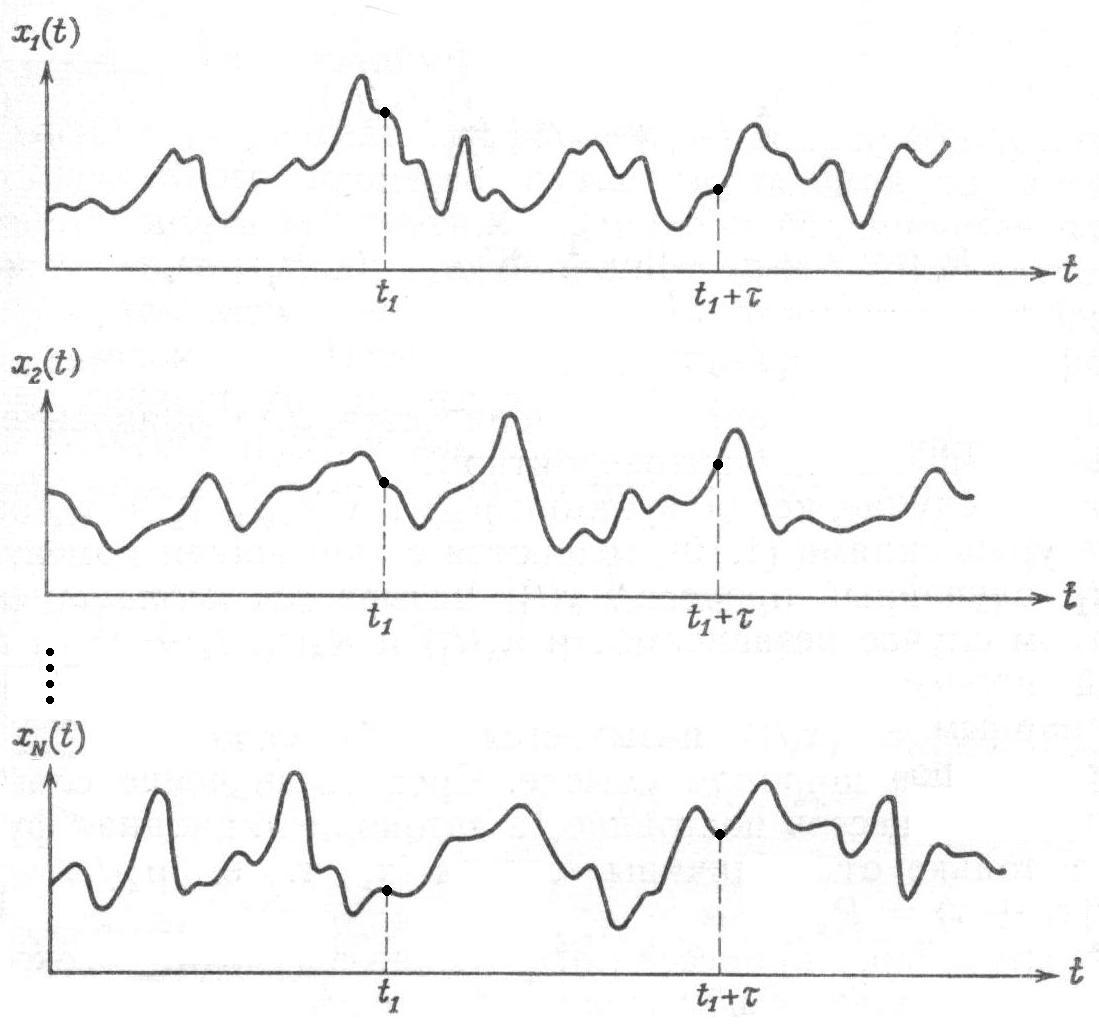
Рассмотрим множество выборочных функций случайного процесса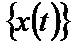 
(рисунок 1.7) и введем понятия среднего значения и ковариационной функции СП.
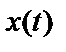– выборочная функция, 
– количество выборочных функций,
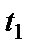– момент усреднения, 
– временной сдвиг между точками СП
Рисунок 1.7 – Множество выборочных функций СП
Среднее значение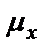 
случайного процесса 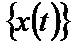в момент времени 
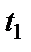находят путем суммирования мгновенных значений каждой выборочной функции в момент времени 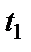и деления полученной суммы на число выборочных функций:
, (1.11)
где 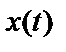– выборочная функция;
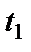– момент усреднения;
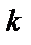– номер выборочной функции;
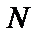– количество выборочных функций.
Ковариационная функция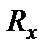 
случайного процесса 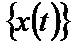представляет собой усредненное произведение мгновенных значений случайного процесса в два момента времени, отстоящие друг от друга на интервал :
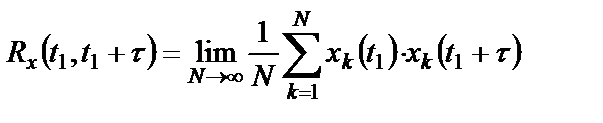. (1.12)
Введенные выше функции (1.11), (1.12) определяются по ансамблю выборочных функций, поэтому способ усреднения носит названия усреднения по ансамблю.
Если среднее значение и ковариационная функция случайного процесса изменяются с течением времени 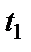, то процесс считается нестационарным. Если же названные функции не зависят от момента усреднения 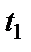, то процесс относится к стационарным процессам.
Для слабо стационарного случайного процесса справедливы следующие соотношения для среднего значения и ковариационной функции:
1. 
;
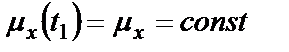2. 
.
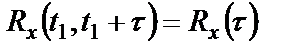При дополнительной независимости ковариационной функции процесса еще и от временного сдвига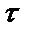 
, процесс считается строго стационарным:
1. 
;
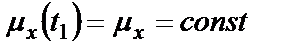2. 
.
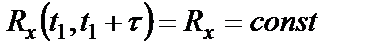Дата добавления: 2015-08-14; просмотров: 658;