Полигармонические процессы

В большинстве своем полигармонические процессы могут быть представлены в виде ряда Фурье

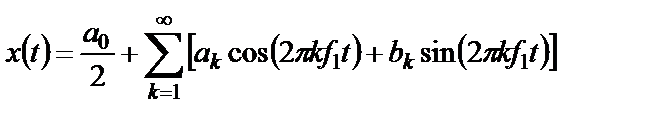, (1.6)

где 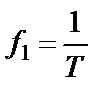– основная частота;

,

,

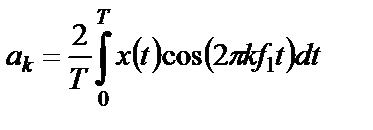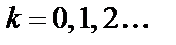
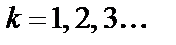
Возможен и другой способ записи ряда Фурье для полигармонического процесса:

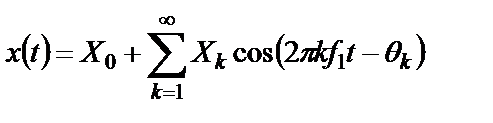, (1.7)

где ;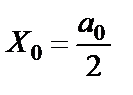

, ,

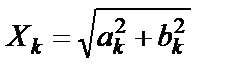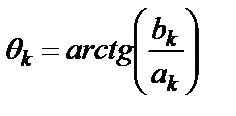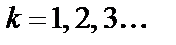
Как видно из формулы (1.7), полигармонический процесс состоит из постоянной составляющей 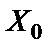и бесконечного числа синусоидальных компонент, называемых гармониками, с амплитудами 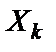и начальными фазами 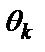. Частоты всех гармоник кратны основной частоте , т.е. соизмеримы.

Очевидно, что гармонический процесс является частным случаем полигармонического процесса при .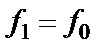

На практике при анализе периодических процессов начальные фазы часто во внимание не принимаются. В этом случае формуле (1.7) соответствует дискретный спектр, представленный на рисунке 1.3.

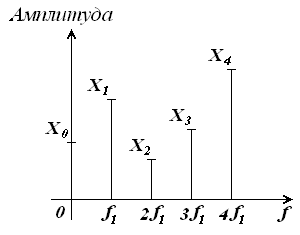
Рисунок 1.3 – Спектр полигармонического процесса

Физические явления, которым соответствуют полигармонические процессы, встречаются гораздо чаще явлений, описываемых простой гармонической функцией.