Эргодические случайные процессы
Случайный процесс может быть описан не только путем усреднения значений процесса в отдельные моменты времени (т.е. усреднением по ансамблю), возможно также его описание путем усреднения по времени наблюдения одной выборочной функции (рисунок 1.8).
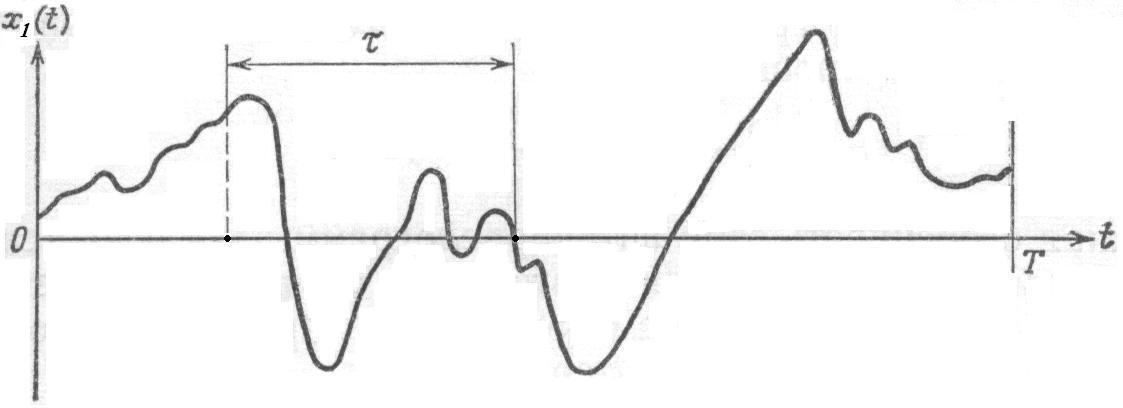
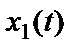– выборочная функция, 
– временной сдвиг между точками СП,
– время наблюдения выборочной функции
Рисунок 1.8 – Выборочная функция СП
Среднее значение и ковариационная функция случайного процесса в этом случае принимают вид:
, (1.13)
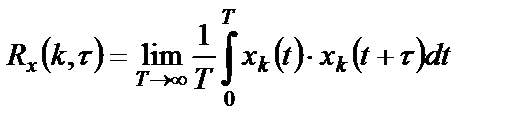, (1.14)
где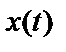 
– выборочная функция;
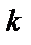– номер выборочной функции;
– время наблюдения выборочной функции.
Такой способ усреднения носит названия усреднения по времени наблюдения.
Если среднее значение и ковариационная функция процесса, рассчитанные по соотношениям (1.13), (1.14), одинаковы для различных выборочных функций (различных номеров реализаций 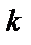), а случайный процесс является стационарным, то он относится к эргодическим случайным процессам.
Для таких процессов справедливы следующие соотношения:
1. 
;
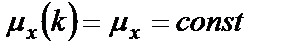2. 
.
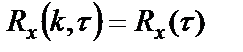Усредненные характеристики эргодических случайных процессов, рассчитанные усреднением по ансамблю выборочных функций и усреднением по времени наблюдения одной выборочной функции, равны между собой.
Введенные выше усредненные характеристики СП могут быть записаны в операторной форме:
,
,
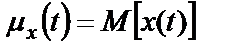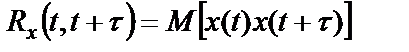где 
– оператор усреднения.
1.2.3 Погрешности выборочных оценок
Рассмотрим еще раз формулы расчета среднего значения случайного процесса путем усреднения по ансамблю выборочных функций
и усреднения по времени наблюдения одной реализации
.
Обе формулы содержат операцию перехода к пределу, которая на практике, конечно, неосуществима, поскольку невозможно обработать бесконечное число реализаций (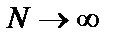 
) или одну реализацию бесконечной длины ( 
). Поэтому анализ случайных процессов дает только выборочные оценки истинных значений их параметров. Необходимо уметь оценивать величину возникающей при этом ошибки.
При обработке случайных процессов ошибки подразделяют на случайные и систематические.
Случайные ошибки являются следствием разброса значений, полученных по разным выборочным функциям одного случайного процесса. Эти ошибки являются прямым следствием конечности числа реализаций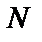 
или времени наблюдения 
. По этой причине случайные ошибки неизбежны.
Величина случайной ошибки обратно пропорциональна корню квадратному из числа реализаций или времени наблюдения:
~ 
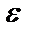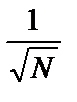или ~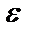 
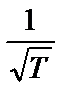. (1.15)
Анализ соотношения (1.15) показывает, что для уменьшения случайной ошибки измерений, например, в два раза необходимо увеличить время обработки реализации или количество выборочных функций в четыре раза.
Абсолютное значение и знак систематических ошибок не изменяется при переходе от одной выборочной функции к другой. Такие ошибки называют также смещением. Смещение часто появляется при приближенном вычислении производных, например при оценивании плотностей вероятности.
Дата добавления: 2015-08-14; просмотров: 801;