Спектральный анализ идеальной системы
Рассмотрим идеальную систему с импульсной характеристикой 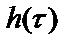 и частотной характеристикой
и частотной характеристикой 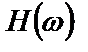 . На вход системы поступает реализация стационарного эргодического случайного процесса
. На вход системы поступает реализация стационарного эргодического случайного процесса 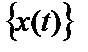 с нулевым средним значением, а на выходе после затухания переходных процессов формируется реализация стационарного процесса
с нулевым средним значением, а на выходе после затухания переходных процессов формируется реализация стационарного процесса  .
.
Рассчитаем произведение мгновенных значений процессов на входе и выходе системы 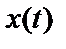 и
и 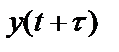 в два различных момента времени с использованием интеграла свертки (2.4):
в два различных момента времени с использованием интеграла свертки (2.4):
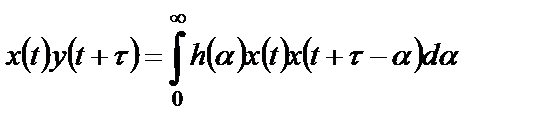 . (2.20)
. (2.20)
Выполнив операцию усреднения над обеими частями равенства (2.20)
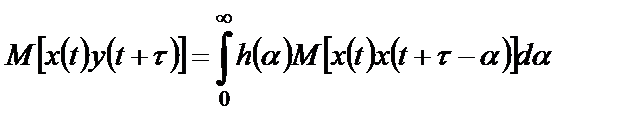 ,
,
получим соотношение для взаимной ковариационной функции входного и выходного процессов в системе:
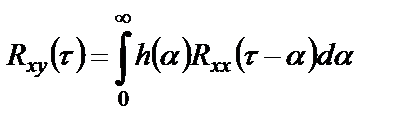 . (2.21)
. (2.21)
Применим прямое преобразование Фурье к соотношению (2.21) и учтем выражения для спектральных плотностей (1.33), (1.35):
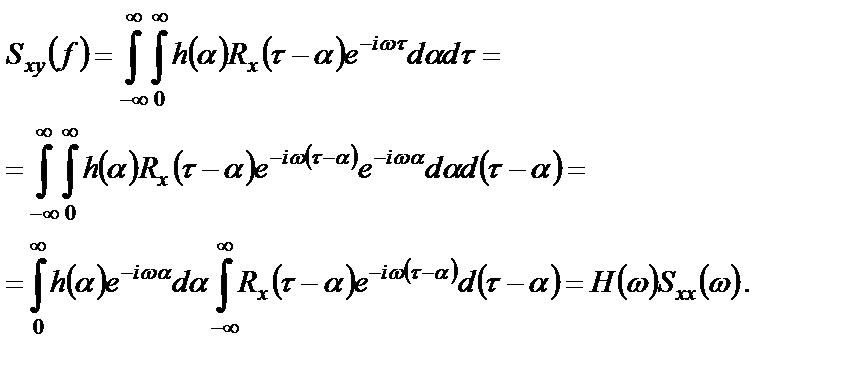
Аналогичные вычисления проведем и для произведения мгновенных значений выходного процесса системы в два различных момента времени:
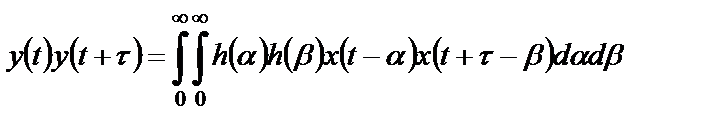 . (2.22)
. (2.22)
После усреднения выражения (2.22) получим
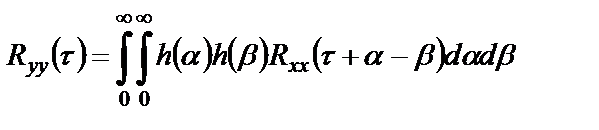 . (2.23)
. (2.23)
Прямое преобразование Фурье над соотношением (2.23) дает
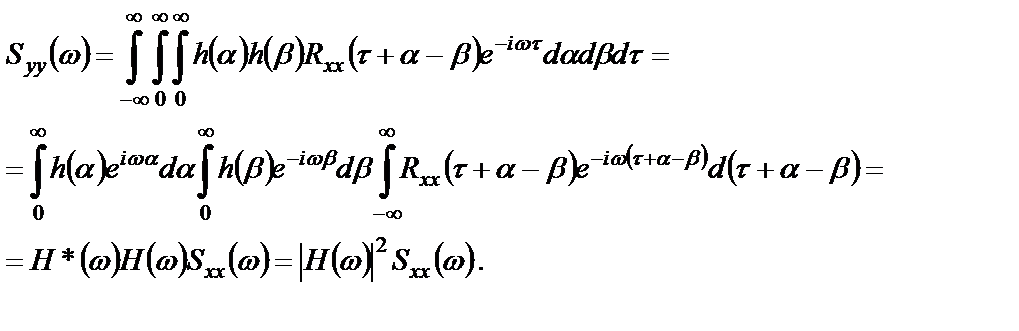
Таким образом, основные спектральные соотношения для идеальной системы, связывающие между собой спектральные плотности на входе и выходе системы, имеют вид:
 (2.24)
(2.24)
Первое из выражений (2.24) является комплексным и называется соотношением для взаимных спектральных плотностей входного и выходного процессов системы, второе выражение – действительным и называется соотношением между спектральными плотностями входного и выходного процессов.
Выражения (2.24) справедливы и для физически измеримых односторонних спектральных плотностей:
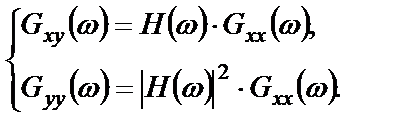 (2.25)
(2.25)
Основные спектральные соотношения можно вывести и без предварительного нахождения ковариационных функций (2.21) и (2.23).
Для любой пары усеченных реализаций достаточно большой длины 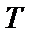 интеграл свертки
интеграл свертки

в результате финитного преобразования Фурье (1.48)
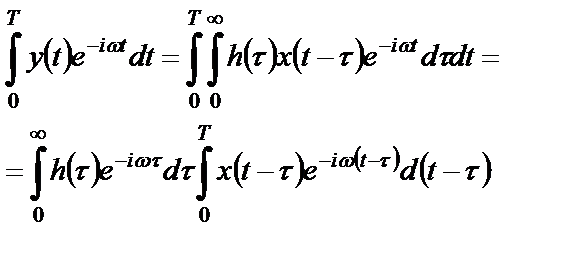
преобразуется в эквивалентное равенство
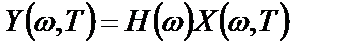 . (2.26)
. (2.26)
Тогда справедливы следующие соотношения:
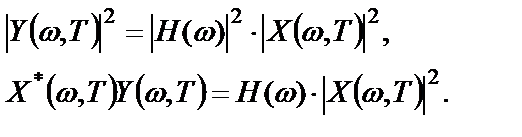 (2.27)
(2.27)
Если теперь выражения (2.27) усреднить по ансамблю реализаций, умножить на величину 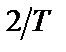 и устремить
и устремить 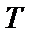 к бесконечности, то из соотношений (1.51) получим формулы (2.25):
к бесконечности, то из соотношений (1.51) получим формулы (2.25):
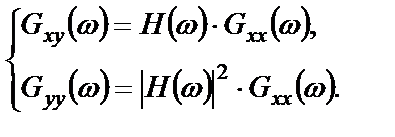
Дата добавления: 2015-08-14; просмотров: 649;
