Функция обычной когерентности

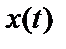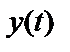Функция обычной когерентности (используются также функции частной и множественной когерентности) между процессами и представляет собой действительную величину, которая уже была определена формулой (1.47):

,

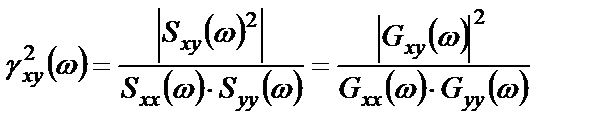причем .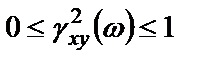

Для идеальной системы справедливо равенство .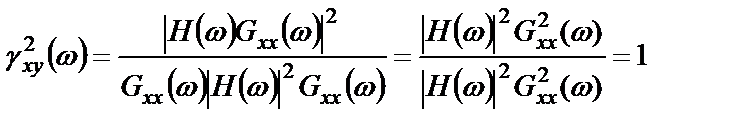

Следовательно, в случае линейной системы с постоянными параметрами и одним входом при полном отсутствии помех функция когерентности равна единице.

С другой стороны, если процессы и совершенно не коррелированы, т.е. 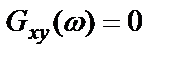для всех 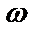, то функция когерентности 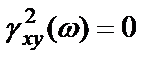для всех .

Если же функция когерентности принимает промежуточные между нулем и единицей значения, то практически может иметь место одна или несколько следующих возможностей:

1. в измерениях присутствует внешний шум;

2. оценки спектров мощности смещены из-за недостаточного разрешения по частоте;

3. система, преобразующая 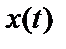в 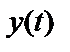, не линейна;

4. на выходной процесс 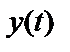влияют и другие входные процессы кроме .

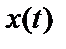Важное и полезное свойство функции когерентности заключается в том, что она сохраняется при линейных преобразованиях.

Предположим, что 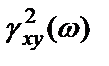– функция когерентности между 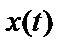и 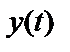, которую необходимо определить. Пусть 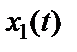– линейное преобразование 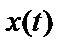, а 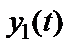– линейное преобразование 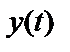, тогда

.

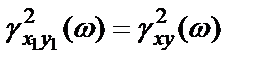Таким образом, для измерения 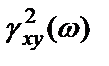можно использовать наблюдения 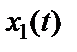вместо 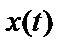и (или) наблюдения 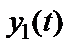вместо 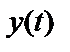, если по каким-либо причинам это проще или удобнее в конкретной задаче.