Система с обратной связью

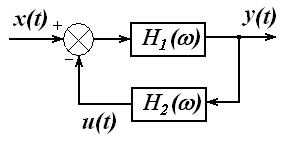
Рассмотрим идеальную систему с отрицательной обратной связью (рисунок 2.6). На схеме , 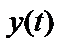– наблюдаемые процессы на входе и выходе системы, 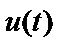– ненаблюдаемый процесс на выходе тракта обратной связи с частотной характеристикой 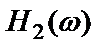, 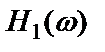– частотная характеристика прямого тракта.

Если частотная характеристика тракта обратной связи равна нулю

,

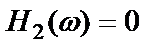то модель сводится к системе с одним входом и одним выходом (п.2.3).

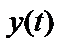, – наблюдаемые процессы на входе и выходе;

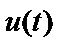– ненаблюдаемый процесс на выходе обратной связи;

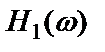– частотная характеристика прямого тракта;

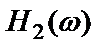– частотная характеристика тракта обратной связи

Рисунок 2.6 – Система с обратной связью

Выясним изменения, вносимые такой схемой в полученные ранее результаты.

Интегралы свертки для процессов на входе и выходе прямого и обратного трактов имеют соответственно вид

,

.

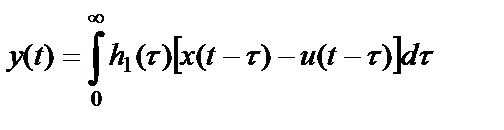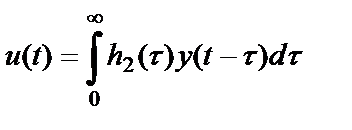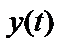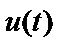Тогда финитные преобразования Фурье над , и при достаточно большой длине реализаций связаны между собой соотношением

,

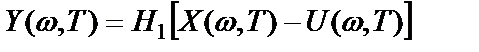где

.

Поэтому

,

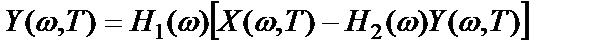откуда частотная характеристика системы равна

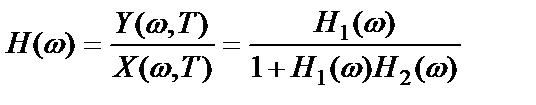. (2.51)

Величина 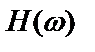– это общая частотная характеристика системы с цепью обратной связи, связывающая процессы и 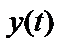, которая может быть определена по наблюдениям только и 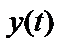. При этом на всех частотах должно выполняться следующее неравенство:

.

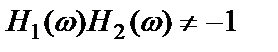Экспериментальное определение частотных характеристик отдельных трактов 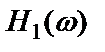и 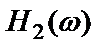невозможно, если величина на выходе обратной связи 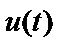не наблюдаема. Однако, ес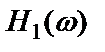ли или 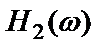известна или есть основания предполагать вид одной из этих характеристик, то вторую величину можно найти.

Например, пусть частотная характеристика обратной связи является известной положительной константой .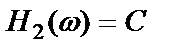

Тогда

,

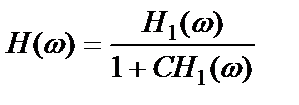откуда

. (2.51)

Частотную характеристику системы 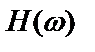можно найти по взаимной спектральной плотности

,

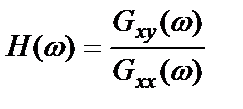поэтому

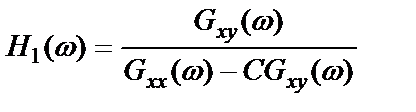. (2.52)

Очевидно, что характеристик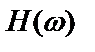и и 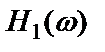не совпадают, если .

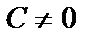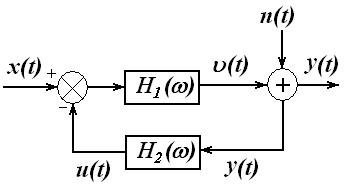
Предположим теперь, что некоррелированный внешний шум попадает на выходе в систему с обратной связью (рисунок 2.7).

В такой системе 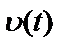– выходной процесс прямого тракта с частотной характеристикой 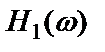, который отдельно не может быть измерен. Вместо него наблюдается процесс

,

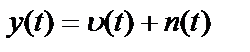где 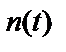– некоррелированный шум.

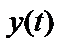, – наблюдаемые процессы на входе и выходе системы;

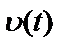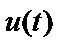, – ненаблюдаемые процессы на выходе прямого и обратного трактов; 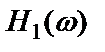, 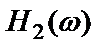– частотные характеристики прямого и

обратного трактов; 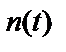– ненаблюдаемый шум на выходе системы

Рисунок 2.7 – Система с обратной связью при наличии шума на выходе

Выходной процесс 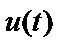тракта обратной связи с частотной характеристикой 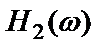также не может быть измерен непосредственно.

Применив к реализациям достаточно большой длины 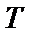финитное преобразование Фурье, получим следующие соотношения:

,

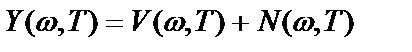где ,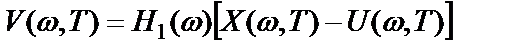

.

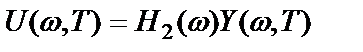Поэтому

,

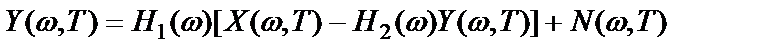откуда реакция системы с обратной связью равна

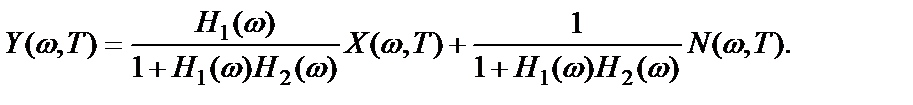(2.53)

Первое слагаемое в выражении (2.53) определяет вклад полезного сигнала, второе слагаемое – вклад шума.

Отношение сигнала к шуму на выходе системы соответственно равно

,

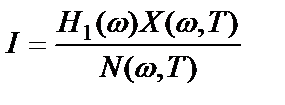откуда видно, что оно является функцией от частотной характеристики прямого тракта 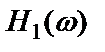и не зависит от характеристики обратного тракта 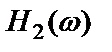. Поэтому отношение сигнала к шуму растет с увеличением 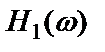при фиксированном значении 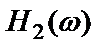, что представляет собой полезное свойство систем с обратной связью.

Выражение (2.53) может быть представлено в виде

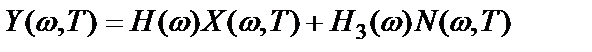, (2.54)

где ,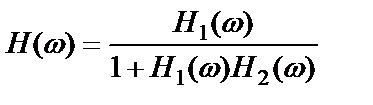

.

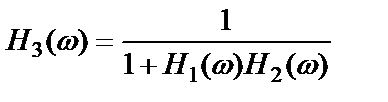Тогда суммарный выходной спектр мощности в системе с обратной связью равен

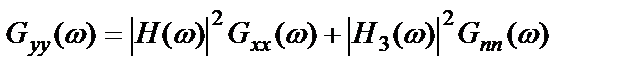. (2.55)

Из формул (2.34) и (2.55) следует, что функция когерентности между и определяется как

. (2.56)

Таким образом, 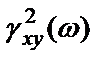не является функцией от 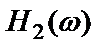, что находится в согласии с тем, что отношение сигнала к шуму на выходе системы с обратной связью не зависит от частотной характеристики тракта обратной связи.