Спектральные соотношения

Пусть система состоит из одного стационарного эргодического случайного процесса 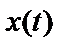, который вызывает 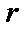наблюдаемых выход-ных процессов 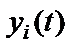, , 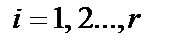искаженных некоррелированным шумом (рисунок 3.1). Пунктиром на рисунке выделена система, имеющая 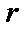трактов распространения входного сигнала с частотными характеристиками , .

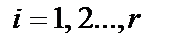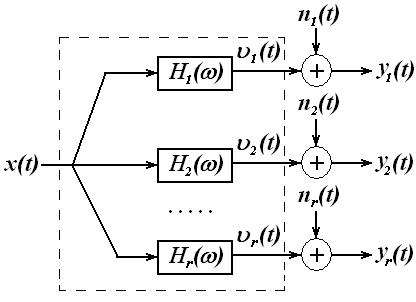
– входной процесс; – частотная характеристика i-го тракта;

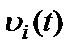– ненаблюдаемый истинный выходной процесс i-го тракта;

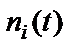– ненаблюдаемый шум на выходе i-го тракта;

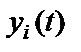– наблюдаемый выходной процесс i-го тракта;

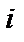– номер тракта распространения сигнала в системе

Рисунок 3.1 – Система с одним входом и несколькими выходами

Для каждого i-го тракта распространения сигнала выходной процесс имеет вид

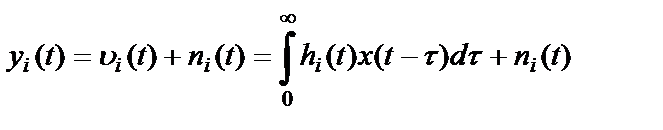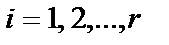, . (3.1)

Выполнив финитное преобразование Фурье над реализацией достаточно большой длины 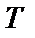, получим

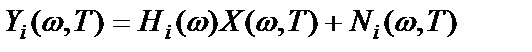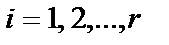, , (3.2)

откуда, с учетом некоррелированности шума, спектральная плотность на выходе тракта определится как

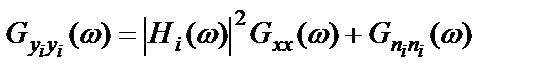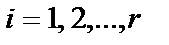, . (3.3)

Для взаимной спектральной плотности процессов 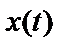и 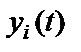аналогично получим

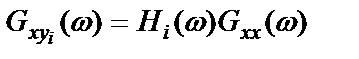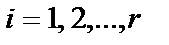, . (3.4)

Соотношения (3.3), (3.4) для i–го тракта рассматриваемой системы в точности совпадают со спектральными соотношениями (2.31), (2.32) для системы с одним входом и одним выходом при наличии внешнего шума на выходе.

Используя формулу (3.2) для различных трактов с номерами i и j, можно получить взаимную спектральную плотность между двумя любыми выходными процессами

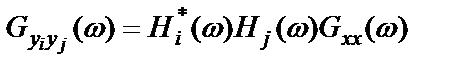. (3.5)

Отсюда следует, что наблюдение взаимной спектральной плотности 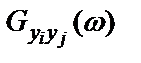и знание частотных характеристик отдельных трактов и 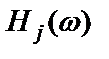позволяют оценить спектральную плотность входного процесса , даже если он ненаблюдаем.